Sum
【问题描述】
给定一个正整数 N ( N <= 231 - 1 )
求:
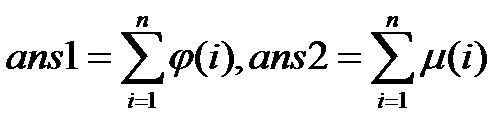
【输入格式】
一共T+1行
第1行为数据组数T(T<=10)
第2~T+1行每行一个非负整数N,代表一组询问
【输出格式】
一共T行,每行两个用空格分隔的数ans1,ans2
【样例输入】
6
1
2
8
13
30
2333
【样例输出】
1 1
2 0
22 -2
58 -3
278 -3
1655470 2
题解:
首先推一波式子
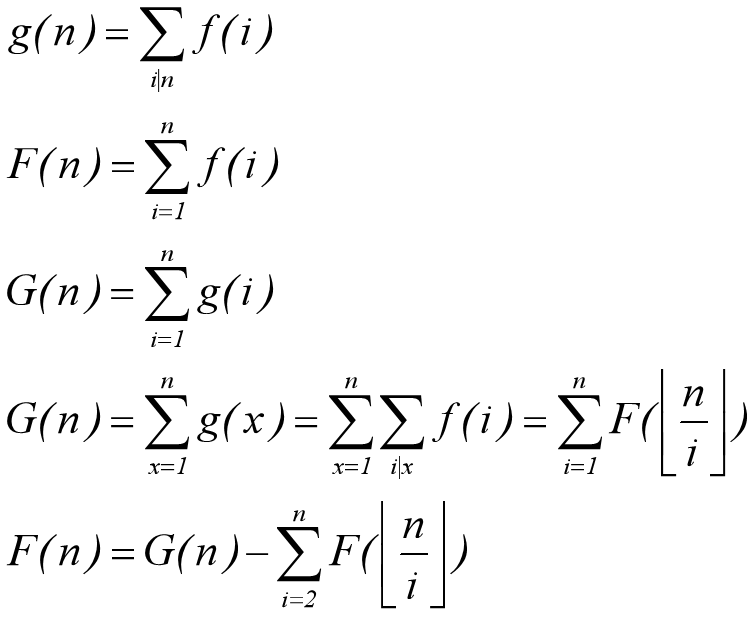
上式就是杜教筛的原理
![]()
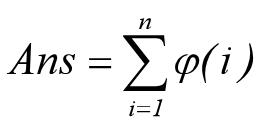 :
:
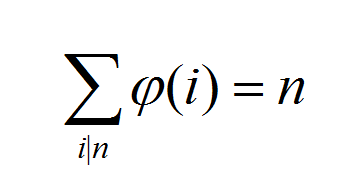
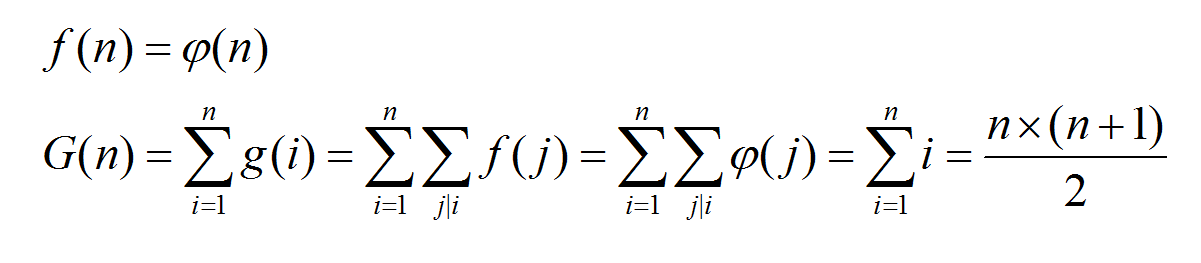
 :
:

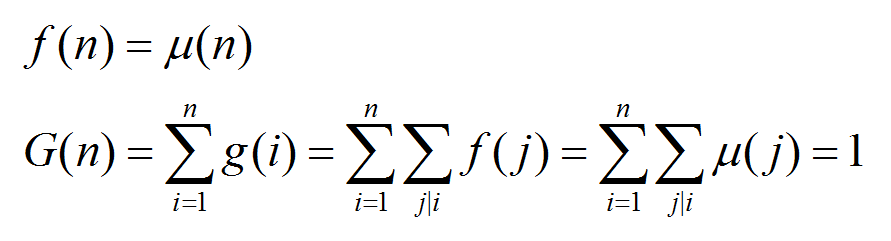
对于![]() 的求解方式在上面已经给出了
的求解方式在上面已经给出了
那么求出前![]() 项答案并记忆化状态,就能达到
项答案并记忆化状态,就能达到![]() 的时间复杂度
的时间复杂度
由于 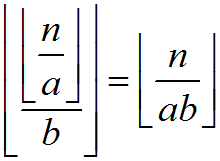 ,那么我们求的每一项的参数都是
,那么我们求的每一项的参数都是 ![]() 形式的
形式的
对于 ![]() 小于等于
小于等于![]() 的答案我们已经预处理出了
的答案我们已经预处理出了
所以我们只需要记忆大于![]() 的答案
的答案
首先提出一个命题:对于 ![]() ,
,![]() 都不相同
都不相同
证明:
假设 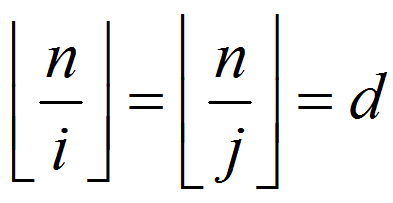 ,且
,且![]()
那么![]()
mi , mj 表示两者的余数,它们的差为![]()
因为![]() ,所以
,所以![]()
那么![]() ,而
,而![]() ,假设不成立
,假设不成立
所以不存在![]() ,使得
,使得![]()
证毕
所以在 ![]() 时,
时,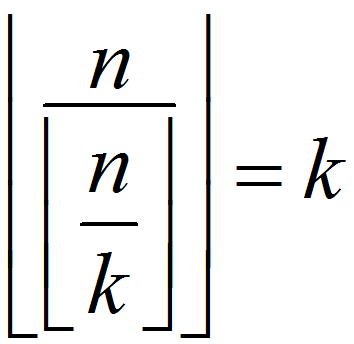 成立
成立
那么![]() ,我们就能直接使用数组存,对于每一个参数,我们将其除k的结果作为下标储存答案
,我们就能直接使用数组存,对于每一个参数,我们将其除k的结果作为下标储存答案
1 #include<cmath>
2 #include<cstdio>
3 #include<cstdlib>
4 #include<cstring>
5 #include<iostream>
6 #include<algorithm>
7 using namespace std;
8 const int maxm = 2e6 + 1;
9 const int maxn = 1e4 + 1;
10 int n;
11 int pri[maxm];
12 bool vis[maxm];
13 struct couple
14 {
15 long long miu, phi;
16 };
17 couple ans[maxn], ori[maxm];
18 inline void Scan(int &x)
19 {
20 char c;
21 bool o = false;
22 while(!isdigit(c = getchar())) o = (c != '-') ? o : true;
23 x = c - '0';
24 while(isdigit(c = getchar())) x = x * 10 + c - '0';
25 if(o) x = -x;
26 }
27 int m;
28 inline void Sieve()
29 {
30 int tot = 0;
31 m = maxm - 1;
32 ori[1] = (couple) {1, 1};
33 for(int i = 2; i <= m; ++i)
34 {
35 if(!vis[i])
36 {
37 pri[++tot] = i;
38 ori[i] = (couple) {-1, i - 1};
39 }
40 for(int j = 1; j <= tot; ++j)
41 {
42 int k = pri[j];
43 long long s = (long long) i * k;
44 if(s > m) break;
45 vis[s] = true;
46 if(!(i % k))
47 {
48 ori[s].miu = 0;
49 ori[s].phi = ori[i].phi * k;
50 break;
51 }
52 else
53 {
54 ori[s].miu = -ori[i].miu;
55 ori[s].phi = ori[i].phi * ori[k].phi;
56 }
57 }
58 }
59 for(int i = 1; i <= m; ++i)
60 {
61 ori[i].miu += ori[i - 1].miu;
62 ori[i].phi += ori[i - 1].phi;
63 }
64 }
65 couple Solve(int x)
66 {
67 if(x <= m) return ori[x];
68 int e = n / x;
69 if(vis[e]) return ans[e];
70 int last;
71 couple c, s;
72 s.miu = 1, s.phi = x * ((long long) x + 1) >> 1;
73 for(long long i = 2; i <= x; i = (long long) last + 1)
74 {
75 last = x / (x / i);
76 c = Solve(x / i);
77 s.miu -= c.miu * (long long) (last - i + 1), s.phi -= c.phi * (long long) (last - i + 1);
78 }
79 vis[e] = true, ans[e] = s;
80 return s;
81 }
82 int main()
83 {
84 int T;
85 Scan(T);
86 Sieve();
87 while(T--)
88 {
89 Scan(n);
90 memset(vis, false, sizeof(vis));
91 if(n <= m) printf("%lld %lld
", ori[n].phi, ori[n].miu);
92 else
93 {
94 couple answer = Solve(n);
95 printf("%lld %lld
", answer.phi, answer.miu);
96 }
97 }
98