程序验证本福特定律

一、定义

本福特定律，也称为本福德法则，说明一堆从实际生活得出的数据中，以1为首位数字的数的出现机率约为总数的三成，接近期望值1/9的3倍。推广来说，越大的数，以它为首几位的数出现的机率就越低。它可用于检查各种数据是否有造假。[1]

二、数学

本福特定律说明在b进位制中，以数n起头的数出现的概率为

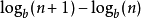
本福特定律不但适用于个位数字，连多位的数也可用。
在十进制首位数字的出现概率（%，小数点后一个位）：

d	p
1	30.1%
2	17.6%
3	12.5%
4	9.7%
5	7.9%
6	6.7%
7	5.8%
8	5.1%
9	4.6%

三、证明

其实对于本福特定律，到目前为止还没有公认的证明。

大部分数据能够满足，也有部分数据是不满足的，比如均匀分布的数据

1、很多数据的增长量会正比于存量（类似银行的存款业务，存的越多，收益越多）会有这么一个公式：

ΔN/(N*Δt)=const（常数）

其中ΔN是增量，Δt是单位时间，N是存量

2、增长是指数增长，即相同时间内，翻的倍数是相同的，有

N=N0*e^(ct)

其中，当存量N0增长到N的时候，需要 t 时间，c是常数

可知，当N1增长到N2的时候，需要的时间是：

t = c'lg(N2/N1)

3、计算

t1 = c'lg(2)

t2 = c'lg(3/2)

...

tn = c'lg(n+1)/n

验证下数据首位从 1~9 所需要的时间

t = t1 + t2 + ... + t9 = c'lg(10) = c'

P1 = t1 / t = c'lg(2)/c' = lg(2) = lg(1+1)/1 ≈ 30.1%

Pn = tn / t = lg(n+1)/n

这里联想到老祖宗的一句话，万事开头难，或许是这个意思吧。其实这个定律到目前为止还没有一个公认的证明，只是很多数据是符合本福特定律的。

四、验证

验证本福特定律对数字有一定的要求，必须是杂乱无章的数据，比如国家人口、GDP等

下面用斐波那契数列和随机数验证下

1、斐波那契数列验证

PHP：

<?php
$size = 1000;
$arr = array(1, 2);
for($i = 2; $i < $size; $i++) {
    $arr[] = $arr[$i-1] + $arr[$i-2];
}
$sum = array(0, 0, 0, 0, 0, 0, 0, 0, 0, 0);
for($k = 0; $k < count($arr); $k++) {
    $index = substr($arr[$k], 0, 1);
    $sum[$index]++;
}
print_r($sum);
for($n = 1; $n < count($sum); $n++) {
    echo "首位 {$n} ,比例 " . round($sum[$n]/$size, 2) . "
";
}
?>

输出：

Array
(
    [0] => 0
    [1] => 300
    [2] => 177
    [3] => 125
    [4] => 96
    [5] => 80
    [6] => 67
    [7] => 57
    [8] => 53
    [9] => 45
)
首位 1 ,比例 0.3
首位 2 ,比例 0.18
首位 3 ,比例 0.13
首位 4 ,比例 0.1
首位 5 ,比例 0.08
首位 6 ,比例 0.07
首位 7 ,比例 0.06
首位 8 ,比例 0.05
首位 9 ,比例 0.05

2、随机数，注意，程序的随机数是伪随机数，这里加上一个随机的增长率，此外还要注意数据可能会太长导致越界，加个循环保证随机数不超过十的十五次方

PHP：

<?php
$count = 0;
$size = 1000;
$grow = 80000;//增长率
$a = rand();
$sum = array(0, 0, 0, 0, 0, 0, 0, 0, 0, 0);
for ($i = 0; $i < $size; $i++) {
    //模拟自然增长率，8w可改 
    $k = (rand() - 16384) / $grow + 1;
    $a = $a + $k * $a; 
    while (mb_strlen($a) >= 15) {
        //降下数量级对首位无影响
        $a /= 10;
    }
    $index = substr($a, 0, 1);
    $sum[$index]++;
}
print_r($sum);
for($n = 1; $n < count($sum); $n++) {
    echo "首位 {$n} ,比例 " . round($sum[$n]/$size, 2) . "
";
}
?>

输出：

Array
(
    [0] => 0
    [1] => 303
    [2] => 176
    [3] => 121
    [4] => 111
    [5] => 89
    [6] => 65
    [7] => 54
    [8] => 36
    [9] => 45
)
首位 1 ,比例 0.3
首位 2 ,比例 0.18
首位 3 ,比例 0.12
首位 4 ,比例 0.11
首位 5 ,比例 0.09
首位 6 ,比例 0.07
首位 7 ,比例 0.05
首位 8 ,比例 0.04
首位 9 ,比例 0.05

 五、结论

对于斐波那契数列和随机数，得出来的结果是比较接近于本福特定律的，这也就是本福特定律大多数情况下可以用来验证数据是否造假的原因

参考：

[1]. 本福特定律