某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。
但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。
某天,雷达捕捉到敌国的导弹来袭。
由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数,导弹数不超过1000),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
输入格式
共一行,输入导弹依次飞来的高度。
输出格式
第一行包含一个整数,表示最多能拦截的导弹数。
第二行包含一个整数,表示要拦截所有导弹最少要配备的系统数。
输入样例:
389 207 155 300 299 170 158 65
输出样例:
6 2
分析:
这道题的题意就是,找单调下降最长的长度,然后如果第一遍找不完,再从剩下的导弹高度里边在进找,直到找到所有严格单调下降的导弹高度,并统计找的次数
换句人话--->用多少个单调下降子序列把完整的序列覆盖掉
贪心的流程:
从前往后扫描每个数:
case 1:如果现有的子序列都小于当前的数,就创建一个新的子序列
case 2:将当前数放在大于等于它的最小子序列后面

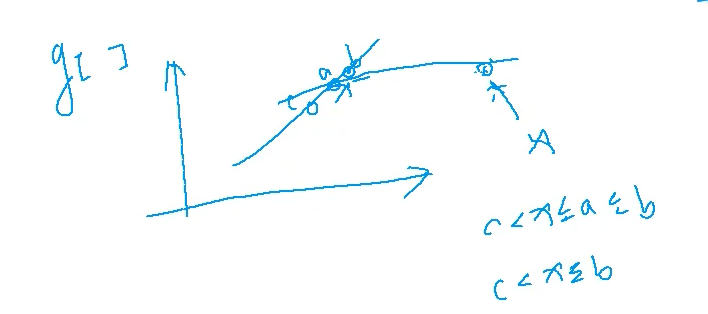
这个g[]数组 就相当于我们的子序列末尾的数,他要保证单调上升,而我们的a就是当前子序列末尾的大于等于x的最小值,也就是将x放在了子序列结尾大于等于x的子序列的后面,也就是a的后边;
这道题如果深挖的化有一个反链的叫做DailWorth定理,有兴趣的可以了解下,在这里我就不赘述了。
这里的输入比较特别可以参考下c++的stringstream

具体详解代码:
1 #include<iostream> 2 #include<algorithm> 3 4 using namespace std; 5 const int N = 1010; 6 int n; 7 int q[N]; 8 int f[N],g[N]; 9 10 int main(){ 11 while(cin >> q[n]) n++; 12 int res = 0; 13 for(int i = 0;i < n;i++){ 14 f[i] = 1; 15 for(int j = 0;j < i;j++) 16 if(q[j] >= q[i]) f[i] = max(f[i],f[j] + 1); 17 res = max(res,f[i]); 18 } 19 cout << res << endl; 20 21 //用g[]数组存储我们当前现有的所有的子序列 22 //用cnt表示我们当前现有子序列的个数 23 int cnt = 0; 24 //从前往后贪心一遍 25 for(int i = 0;i < n;i++){ 26 int k = 0;//k表示我们从前往后找的序列 27 //只要我们没有遍历完所有的序列 并且 当前的序列的结尾小于我们当前的数,就k++ 28 while(k < cnt && g[k] < q[i]) k++;//序列找完并且没有比序列最小值小的我们的序列就++ 29 g[k] = q[i];//将大的q[i]交换到本来小的序列的位置上在进行判断 30 if(k >= cnt) //说明我们没有任何一个序列是大于我们的当前数的 31 //我们就开一个新的序列 32 cnt++; 33 } 34 35 cout << cnt; 36 37 }