| 模型种类 | 模型 | 图示 | 补充 |
|---|---|---|---|
| 线性模型 | 一般线性模型:  , x为向量向量时: , x为向量向量时: 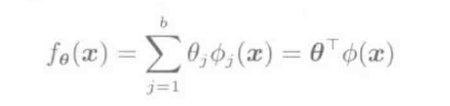 |
 |
多维基函数构造: 1.乘法模型: 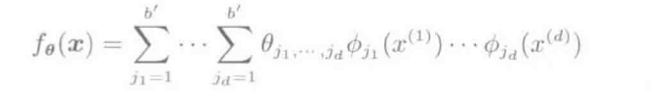 2.加法模型: 2.加法模型: 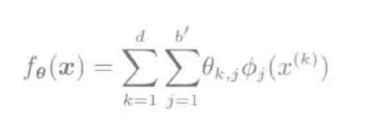 二者对比:乘法模型表现力丰富,但易引入维数灾难;加法模型参数个线性增长,但表现力不足: 二者对比:乘法模型表现力丰富,但易引入维数灾难;加法模型参数个线性增长,但表现力不足: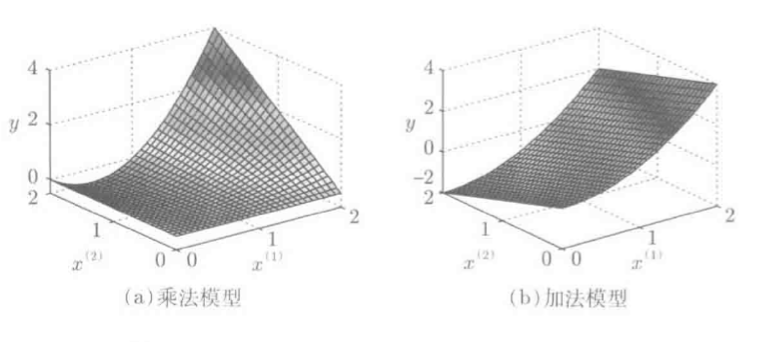 |
| 核模型 | 一般核模型: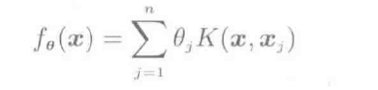 高斯核函数: 高斯核函数: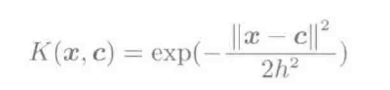 |
一维高斯核模型:  二维高斯核模型: 二维高斯核模型: 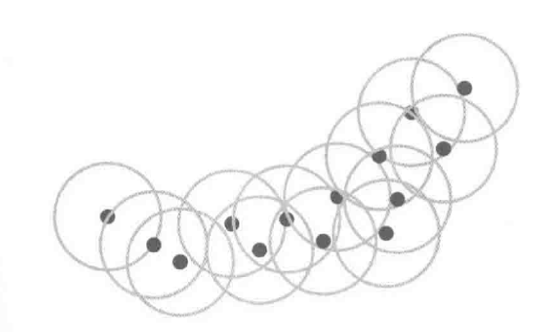 带宽为h, 均值为c的高斯核: 带宽为h, 均值为c的高斯核:  |
1)参数个数不依赖x的维度,由训练样本数n决定,通过计算核均值抑制计算负荷;2)通过核映射可解决非向量样本建模, 如可构建x为字符串,决策树,图表等的核函数 |
| 层级模型 | 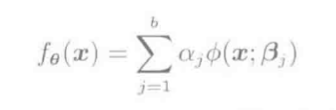 , 其中ϕ(x;β)是含有参数向量β的基函数; 常见的基函数: S型函数 , 其中ϕ(x;β)是含有参数向量β的基函数; 常见的基函数: S型函数 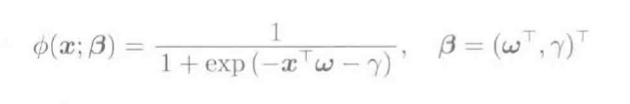 2. 高斯函数: 2. 高斯函数: 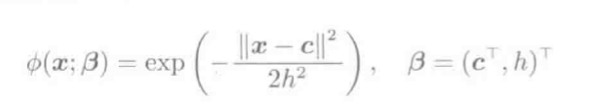 |
三层神经网络: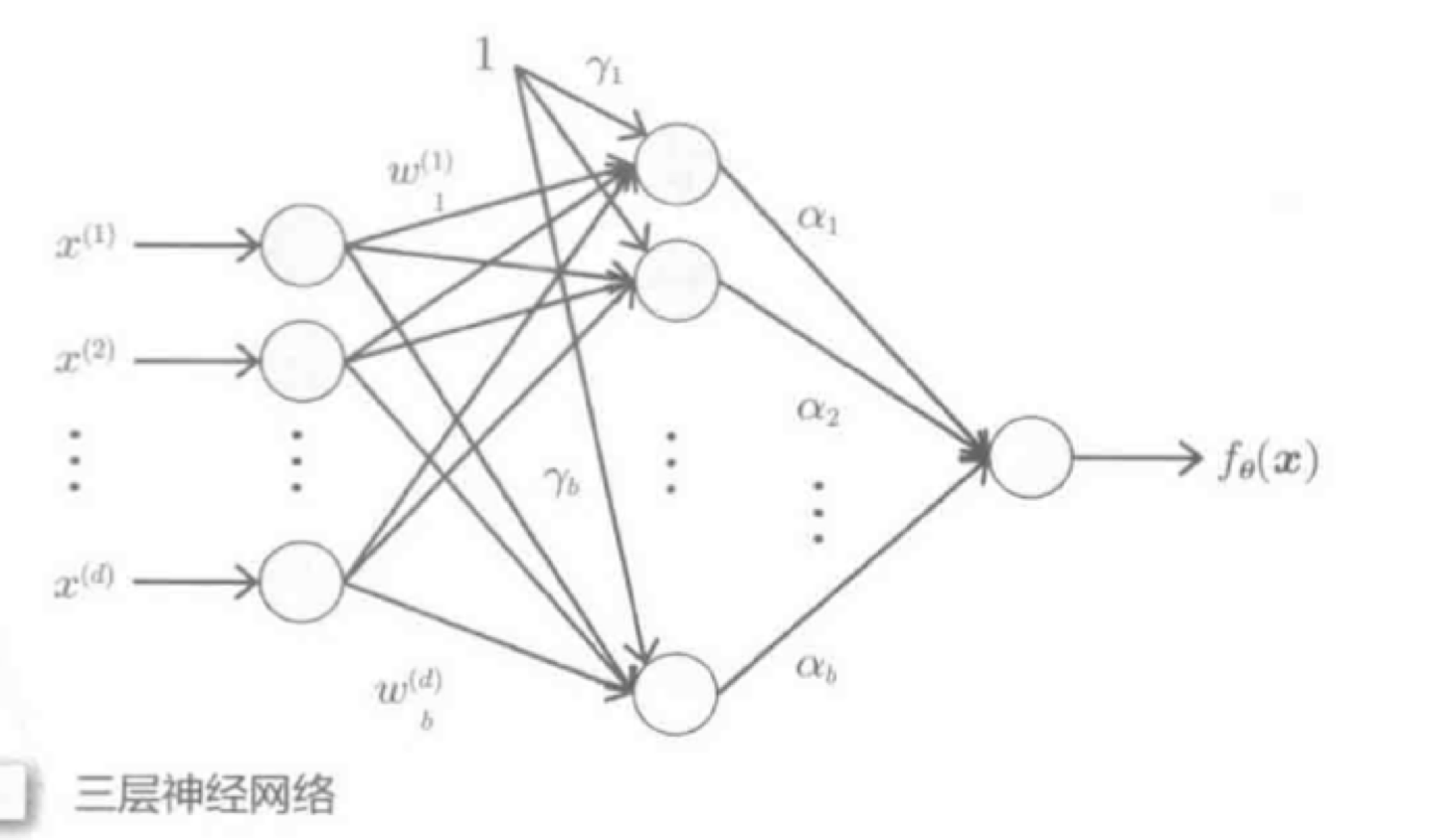 S型基函数: S型基函数: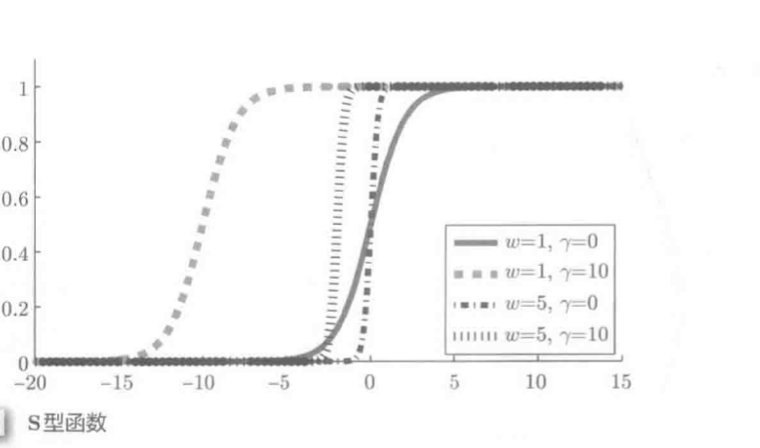 |
层级模型是基于参数向量θ=(α⃗ T,β⃗ T1,βT2,...,βTb)的非线性形式;核模型中高斯函数带宽和均值固定;层级模型中耦合系数{αj}bj=1, 带宽和均值都会被学习; 层级模型参数θ和fθ不是一一对应的(如b=2的人工神经网络):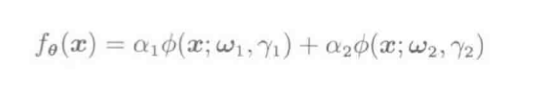 因此模型训练过程非常艰难 因此模型训练过程非常艰难 |
1. 线性模型
一维输入+基函数形式:
fθ(x)=∑j=1bθjϕj(x)=θTϕ(x)
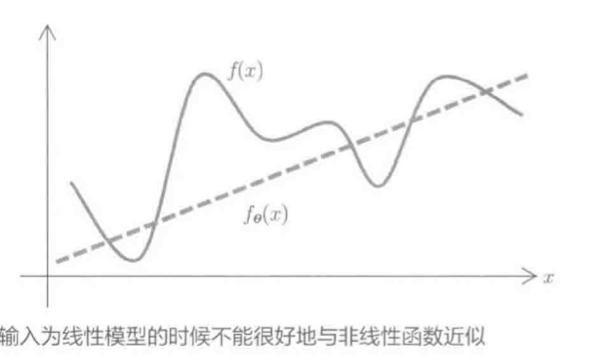
ϕj(x)非线性时, fθ(x)可以表示复杂模型
基函数:
(1) 多项式
ϕ(x)=(1,x,x2,...,xb−1)T
(2)三角多项式
ϕ(x)=(1,sinx,cosx,sin2x,cos2x,...,sinmx,cosmx)T
多维输入形式:
fθ(x⃗ )=∑j=1bθjϕj(x⃗ )=θTϕ(x⃗ )
ϕj(x)是基函数向量ϕ(x)=(ϕ1(x),...,ϕb(x))T)的第j个因子, θj是参数向量θ=(θ1,...,θb)T的第j个因子.
基函数:
(1) 乘法模型
fθ(x⃗ )=∑j1=1b′⋯∑jd=1b′θj1,...,jdϕj1(x(1))⋯ϕjd(x(d))
模型表现力丰富, 其中, b'代表各维参数个数, 参数总和(b′)d, 易导致维数灾难.
(2) 加法模型
θ(x)=∑k=1d∑j=1b′θk,jϕj(x(k))
参数总和b′d, 复杂度小, 表现力差
2. 核模型
线性模型基函数和训练样本无关,核模型的基函数会使用输入样本.
核模型是二元核函数K(⋅,⋅), 以K(x⃗ ,xj)nj=1的方式线性结合:
fθ(x)=∑j=1nθjK(x,xj)
高斯核:
K(x,c)=exp(−∥x−c∥22h2)
, 其中∥⋅∥表示L2范数∥x∥=xTx‾‾‾‾√, h和c是高斯函数带宽和均值
高斯核函数图:
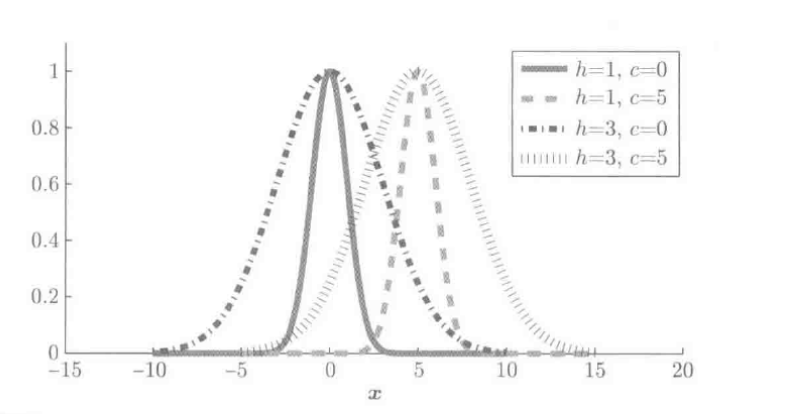
一维高斯核
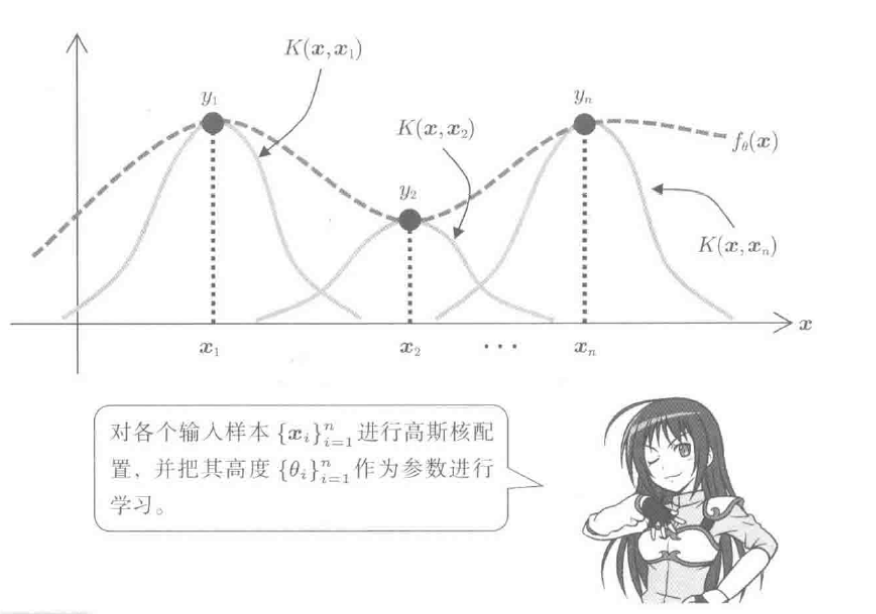
如图, 只在各个样本{xi}ni=1附近近似, 减轻了维数灾难
参数个数不依赖输入变量维数d, 只由样本数n决定
样本数n很大时, 将样本{xi}ni=1的子集{cj}bj=1作为核均值计算, 抑制了计算负荷:
fθ(x)=∑j=1bθjK(x,cj)
核模型是参数向量θ⃗ =(θ1,⋯,θn)T的线性形式, 因此也是基于参数的线性模式的特例.
基于参数的线性模型称为参数模型, 核模型称为非参数模型
核映射: 核模型易扩展,当输入样本不是向量时(字符串,决策树, 图表等),通过构造两个样本x和x'的和核函数K(x,x′)来建模.
3. 层级模型
非线性模型: 和参数相关的不是线性的模型均称为非线性模型
非线性模型中的层级模型:
fθ(x)=∑j=1bαjϕ(x;βj)
上式中, ϕ(x;βj)是包含参数向量β⃗ 的基函数, α⃗ 是参数向量
层级模型是基于参数向量θ⃗ =(α⃗ T,βT1,⋯,βTb)T的非线性形式
S型基函数:
ϕ(x;β)=11+exp(−xTω−γ),β=(ωT,γ)T
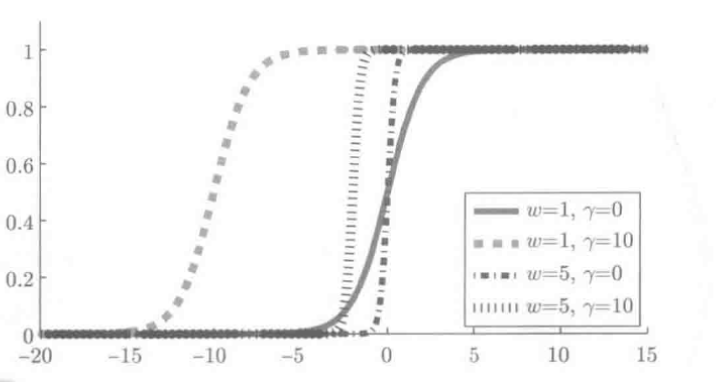
高斯基函数:
ϕ(x;β)=exp(−∥x−c∥22h2),β=(cT,h)T
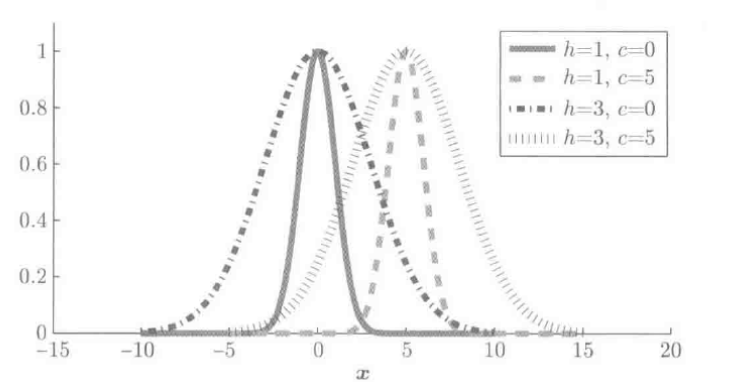
-
使用S型核函数的层级模型称为人工神经网络
-
上式中的高斯函数和核模型中的高斯核相同,但是带宽和均值非固定
-
层级模型会对耦合系数{αj}bj=1,带宽和均值都进行学习, 因此层级模型比核函数更灵活.
-
人工神经网络学习过程艰难: 参数θ和函数fθ不是一一对应的
-
常采用贝叶斯方法学习人工神经网络