[复习资料]网络流学习总结

网络流是个很玄学的东西。

Part One 网络流费用流的算法

1. 网络流常用的算法： FF 、 EK 、 Dinic 、 SAP （未掌握）、 ISAP （未掌握）、 HLPP （未掌握）。

2. 费用流常用的算法： MCMF 、 zkw 费用流（未掌握）。

---

1. FF ：添加反向边，相当于给程序一个反悔的机会（有点像可反悔的贪心？），每次找增广路增广。

2. EK ： FF 的基础上每次找最短路增广。

3. Dinic ：建立分层图，每次增广多条最短路。

4. MCMF ：把 EK 的 dfs 改为 spfa （特殊处理可以变为 dijskra ），每次找最短路增广。

Part Two 一些特殊的网络费用流

1. 无源汇的有上下界的可行流、有源汇的有上下界的最大最小流、无源汇的有上下界的最小最大流、有源汇的有上下界的最小最大费用最小最大流。关键是流量的调整。

2. 有负圈的最小费用流的处理技巧（特殊方法拒绝负圈或者消圈等，未掌握）。

3. 无向平面图的网络流的特殊求法。

---

1. 无源汇的有上下界的可行流/最大最小费用流：流量全部流为下界，建立虚拟源汇，如果某点有多余的流量，从源点连向该点多出的流量，代表有这么多的流量还需要调整，如果某点的流量少了，就从该点连向汇点需要调整的流量，原来的边权设为上界减下界的差值，跑（最大最小费用）最大流，如果流满，说明可行，每边的流量为下界加上残余网络反向边剩下的流量。

2. 有源汇的有上下界的最小最大流/最小最大费用最小最大流：从汇点连向源点上界为 (inf) 下界为 (0) （费用为 (0) ）的边，跑无源汇的有上下界的可行流/最大最小费用流，再去掉虚拟源汇，在残余网络上跑（最小最大费用）最大流，如果是最小流，从汇点往源点跑最大流（相当于把尽量多的多余的流流回去）。

3. 有负圈的最小费用流的处理技巧之消负圈：建立虚拟源汇，将每个点拆为入点和出点，对于原图中的每一个点 (u) ，从 (u) 的出点连向 (u) 的入点、源点连向 (u) 的出点、 (u) 的入点连向汇点流量为 (inf) 费用为 (0) 的边，对于原图一条 (u o v) 流量为 (w) 费用为 (f) 的边，从 (u) 的出点连向 (v) 的入点流量为 (w) 费用为 (f) 的边，然后跑最小费用最大流，将每条边的剩余流量作为其流量进行接下来的操作。可以这样做的原因：保证了每个点的进入的流量都是 (inf) ，流出的流量也都是 (inf) ，满足了流量平横，同时处理后有没有负圈。（注意：可以利用流量均为 (inf) 的技巧来做一些题目，另外，这种特殊的方法可以使得点的入度等于出度，这个方法可以利用在其他题目中）

4. 无向平面图的网络流的特殊求法：利用对偶图，由于有最大流等于最小割，从源点往汇点加一条边记为 (e_0) ，建立对偶图，边权为连接两个平面的边的流量， (e_0) 分开的两个平面作为起点终点，去掉 (e_0) ，那么从起点到终点的每条路径都是原图的一个割，跑最短路即可。

如果您需要进一步的信息或者我糟糕的语文水平无法让您理解上面所说的话，可以看一下这位神仙的博客。

Part Three 网络流的一些经典模型、技巧

利用（最小最大费用）最大流：

1. 直接求最大流。

2. 点有限制流量：拆点。

3. 二分图相关模型：建立源汇，源点向左边的点连边，右边的点向汇点连边，如果点有流量限制，将限制变为它连向源/汇点的边的流量（比如二分图匹配，每个点只能匹配一个点，流量均为 (1) ）。 K-完备匹配：若二分图中每个点的度数都大于等于 K ，则存在 K 个不相交的完全匹配。

   Hall 定理及其证明相关可以看这里。

4. 求混合图的欧拉回路：有向图存在欧拉回路当且仅当每个点入度等于出度，可以类比网络流中的流量平衡，每条边相当于对两个点的流量造成了影响，先给无向边随意定向，再计算出反向给两个点的流量造成的影响，然后用类似计算无源汇的有上下界的可行流的方法进行流量调整。

5. 在有向无环图上选择一些边，直接或间接限制了每个点的入度和出度，求最小费用的一类题目。拆点，将每个点拆为入点和出点，源点连向出点可以出去的流量，入点连向汇点可以进入的流量，对于原图中的一条边 (u o v) ，从 (u) 的出点连向 (v) 的入点一条边，费用看题目意思而定。

   举例：在有向无环图中找到一条经过所有的点的费用最小的路径（相当于限制每个点入度出度为 (1) ，每个点经过一次，相当于进入该点一次，从该点出去一次）；在有向无环图中选择一些边，构成一棵树，限制每个节点的儿子数（每个点父亲仅有一个，入度为 (1) ，儿子最多有题目限制个，出度为该限制）……

6. 加了时间限制的一类问题：可以拆点，将每个点拆成时间数个点。

7. 费用非一次函数的一类问题：拆边，每条边流量设为 (1) ，费用设为流量增加 (1) 费用所增加的值（注意：这里要求费用不降），不必一开始就全拆，可以每次找到增广路后再加边。

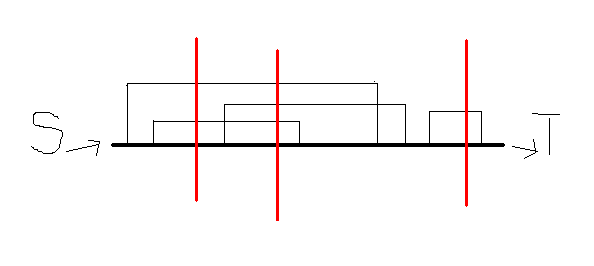
8. 最长 (k) 可重区间集问题：每个点最多被覆盖 (k) 次，可以认为覆盖该点的所有区间流量加起来最多为 (k) ，将点视为边，每边的流量为 (inf) 费用为 (0) ，从源点连向最左端的点流量为 (k) 费用为 (0) ，最右端的点连向汇点流量为 (k) 费用为 (0) ，对于区间([l,r])，连边 (l o r+1) ，流量为 (1) 费用为区间权值，最大费用最大流就是答案。见上图，可以想象流量是一排一排地从 (S) 流向 (T) ，每一排的流量都为 (k) ，由于被视为边的点的流量都为非负数，所以通过上面的边（即区间）的流量最多为k，保证了每点都最多被 (k) 个点覆盖。（注意这题可以出变式，比如每个点覆盖次数即有上限也有下限，每个点覆盖次数不相同等）

   

---

利用最小割

1. 直接求最小割。

2. 一类每个点只有 (0) 和 (1) 两种取值的问题：钦定某个点如果取值为 (0) 则在残余网络中可以从 (S) 遍历到，为 (1) 则不能遍历到，建边 (S) 到 (x) 流量为该点取 (0) 对答案的贡献， (x) 到 (T) 流量为该点取 (1) 对答案的贡献，两者必须割掉一条，然后考虑其他特殊限制：如果 (u) 取 (0) 且 (v) 取 (1) 贡献为 (w) ，则加边 (u o v) 流量为 (w) ； (u) 取 (1) 且 (v) 取 (0) 贡献为 (w) ，则加边 (v o u) 流量为 (w) ；某些点都取 (0) 贡献为 (w) ，则添加一个点 (x) ， (x) 向每个点连流量为 (inf) 的边， (s) 到 (x) 连流量为 (w) 的边；某些点都取 (1) 贡献为 (w) 类似都取 (0) 的情况。处理后答案便是所有贡献之和减去最小割。（还有一些加边加点方法要视题目而定）

3. 最大权闭合子图。

4. 最大密度子图（可以转换为最大权闭合子图加01分数规划）

5. 取值类问题（每个点有 (n) 个取值）：将每个点拆为 (n) 个点，从下到上依次连接，最大取值连到 (T) ， (S) 连最小取值，如果该点选择取值为 (x) ，则表现为取值为 (x) 到取值为 (x+1) 这条边被割断。