T1
题目描述
我们如何评价科学家的成功?根据发表论文的数量或其引用分数——更准确地说,被引用的次数?这两个要素都很重要。如果一篇论文被其他科学家的论文总共引用了C次,那么这篇论文的引用分数为C。科学家成功的一个可能衡量标准是他们的H指数,它同时考虑了论文数量和引用分数。 科学家的H指数定义为具有以下性质的最大整数H:科学家可以选择H篇论文,满足这H篇论文的引用分数都不小于H。例如,如果一个科学家写了10篇论文,并且每一篇都被引用了至少10次,那么他的H指数(至少)是10。 写一个程序,输入某个科学家所有论文的引用分数,输出他的H指数。
输入
第一行输入包含整数N(1≤N≤5*1e5)。表示论文的数量。 第二行输入包含N个自然数Ci(Ci≤1e6)。表示每篇论文的引用分数。
输出
输出一个整数。表示这名科学家的H指数。
样例
样例输入1
5
1 1 4 8 1
样例输出1
2
样例输入2
5
8 5 3 4 10
样例输出2
4
解题思路
此题比较轻松,和大众做法不同,我并没有排序,我用了一个cnt统计数字出现次数,然后倒着来找符合条件的,即积分为i满足能选i篇积分至少为i的。
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
using namespace std;
int n,c,cnt[1000005],maxn;
int sum;
int main(){
//freopen("hindex.in","r",stdin);
//freopen("hindex.out","w",stdout);
scanf ("%d",&n);
for (int i = 1;i <= n;i ++){
scanf ("%d",&c);
cnt[c] ++;
maxn = max(c,maxn);
}
for (int i = maxn;i >= 0;i --){
sum += cnt[i];
if (sum >= i){
printf("%d
",i);
return 0;
}
}
}
T2
题目描述
一个房间里有N张桌子,从左到右排成一行。有些桌子上有电话,而有些桌子是空的。所有的电话都坏了,所以当第i个办公桌上的电话响了,第j个办公桌上的电话也会响,如果第j个办公桌和第i个办公桌的距离不超过D。换句话说,j和i满足|j-i|≤D。第一张桌子和最后一张桌子上一定会有电话。开始的时候,最左边的桌子上的电话会响起。求要让最后一个电话响起,至少要在多少张办公桌上放置新电话?
输入
第一行输入包含两个整数N(1≤N≤3e5)和D(1≤D≤N)。分别表示办公桌的数量和题目中提到的距离。 第二行输入包含了N个整数Ai(0≤Ai≤1)。第i个整数Ai表示第i个张桌子的状态。具体来说,如果Ai=1那么第i张桌子上有电话,如果Ai=0那么第i张桌子上没有电话。
输出
输出一个整数。表示需要放置新电话的数量。
样例
样例输入1
4 1
1 0 1 1
样例输出1
1
样例输入2
5 2
1 0 0 0 1
样例输出2
1
样例输入3
8 2
1 1 0 0 1 0 0 1
样例输出3
2
解题思路
感觉就是一道贪心模拟,我们就直接保证放到最远即可,中途有一些电话线的话,我们就重新开始算。
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
using namespace std;
int n,d,dis,tot;
int vis[300005];
int main(){
//freopen("telefoni.in","r",stdin);
//freopen("telefoni.out","w",stdout);
scanf ("%d%d",&n,&d);
for (int i = 1;i <= n;i ++)
scanf ("%d",&vis[i]);
for (int i = 1;i <= n;i ++){
if (vis[i] == 1)
dis = 1;
else if (dis == d){
tot ++;
dis = 1;
}
else
dis ++;
}
printf("%d",tot);
}
T3
题目描述
年轻的Jozef得到了一个由2的N次方个正整数组成的集合作为礼物。考虑到Jozef经常参加足球锦标赛,他决定为这2的N次方个正整数组织一个锦标赛。 数字锦标赛如下图所示。比赛成对进行,两个数字中较高的一个前进到更高级别。比赛的级别用1到N之间的数字表示,其中最高的级别用数字0表示。
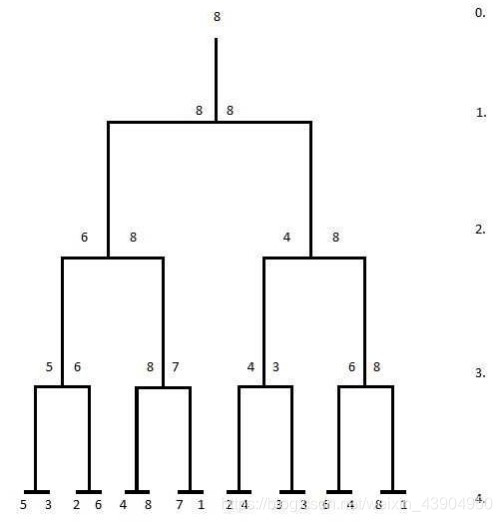
由于Jozef没有时间组织所有的比赛,他想知道,对于集合中的每个数字,在所有的对阵安排中,能达到的最高级别(数字最小的级别)。
输入
第一行输入包含一个整数N(1≤N≤20)。表示题目中提到的N。 第二行输入包含了2的N次方个正整数Ai(Ai≤1e9)。表示集合中2的N次方个正整数。
输出
输出一行包含2的N次方个整数。其中第i个数表示按照输入的顺序集合中的第i个正整数能达到的最高级别。
样例
样例输入1
2
1 4 3 2
样例输出1
2 0 1 1
样例输入2
4
5 3 2 6 4 8 7 1 2 4
3 3 6 4 8 1
样例输出2
1 2 2 1 1 0 1 3 2 1
2 2 1 1 0 3
样例输入3
1
1 1
样例输出3
0 0
解题思路
先说一下题意吧,可能有人觉得样例不对,毕竟当时我一开始也理解错了。
简单来说,他就是让你自己安排,求每一个数最远能到哪。
那我们肯定要排序啊。a的值很大,我们进行离散。
这里有一点是相同的数也可以晋级。所以怎么算其能到达的最远呢。
这里呢,可以找一下规律。
如果i可以到n - 1,那么肯定要有至少2个小于等于i的数。
如果i可以到n - 2,那么肯定要有至少4个小于等于i的数。
如果i可以到n - k,那么肯定要有至少2^k个小于等于i的数。
就这样完了,处理你自己弄一下差不多了。
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
using namespace std;
struct node{
int x,pos;
bool operator < (const node &a)const {
return x < a.x;
}
}s[1500005];
int n,n1,num[1500005],ans[1500005],tot[1500005],sum,cnt;
int qkpow(int x,int y){
int ans = 1;
while (y){
if (y % 2 == 1)
ans = ans * x ;
x = x * x;
y /= 2;
}
return ans;
}
int main(){
//freopen("turnir.in","r",stdin);
//freopen("turnir.out","w",stdout);
scanf ("%d",&n);
n1 = qkpow(2,n);
for (int i = 1;i <= n1;i ++){
int a;
scanf ("%d",&a);
s[i].x = a;
s[i].pos = i;
}
sort(s + 1,s + 1 + n1);
for (int i = 1;i <= n1;i ++){
if (s[i].x != s[i - 1].x){
num[s[i].pos] = ++ cnt;
tot[cnt] ++;
}
else {
num[s[i].pos] = cnt;
tot[cnt] ++;
}
}
for (int i = 1;i <= cnt;i ++){
sum += tot[i];
int j,tot1 = 0;
for (j = 1;j <= n1;j *= 2){
if (sum < j)
break;
tot1 ++;
}
ans[i] = n - tot1 + 1;
}
for (int i = 1;i < n1;i ++)
printf("%d ",ans[num[i]]);
printf("%d
",ans[num[n1]]);
}
T4
题目描述
如果一个数等于它的所有因数(小于自身的)之和,那么这个数就是完美的。例如,28是完美的,因为28=1+2+4+7+14。
基于这个定义,我们数字n的不完美度定为f(n),它等于n与n的所有因数(小于n的)之和的差的绝对值,因此完美数的不完全度为0,其余自然数的不完全度都大于0。
例如:
●f(6)=|6-(1+2+3)|=0
●f(11)=|11-(1)|=10
●f(24)=|24-(1+2+3+4+6+8+12)|=|-12|=12
写一个程序,对于正整数A和B,计算A和B之间所有数字的不完美度之和:即f(A)+f(A+1)+…+f(B)。
输入
第一行输入包含两个整数A和B(1≤A≤B≤1e7)。表示题目中的A和B。
输出
输出一个整数。表示f(A)+f(A+1)+…+f(B)。
样例
样例输入1
1 9
样例输出1
21
样例输入2
24 24
样例输出2
12
解题思路
其实这是一道求约数和的模板题,不完美度这玩意你求出约数和你就可以O(1)时间内求解。
约数和应该来说是有两种求法,第一种便是nlog(n)的求法,代码简短。第二种则是欧拉筛法的求法,代码略长一点,时间复杂度为O(n)。
但考试时限3s,好像nlog(n)并不会爆,评测也过了。但OJ上TLE了,所以还是用欧拉筛吧
代码
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
using namespace std;
int a,b,psum[10000005],cnt,pri[1500005],s[10000005];
bool vis[10000005];
long long ans;
int main(){
scanf ("%d%d",&a,&b);
/*约数个数
for (int i = 2;i <= b;i ++){
if (!vis[i]){
pri[++ cnt] = i;
num[i] = 1;
d[i] = 2;
}
for (int j = 1;j <= cnt && 1ll * i * pri[j] <= b;j ++){
vis[pri[j] * i] = 1;
if (i % pri[j] == 0){
num[pri[j] * i] = num[i] + 1;
d[pri[j] * i] = d[i] / (num[i] + 1) * (num[i] + 2);
break;
}
d[pri[j] * i] = d[i] * 2;
num[i] = 1;
}
}*/
s[1] = 1;
for(int i = 2;i <= b;i ++){
if (!vis[i]){
pri[++ cnt] = i;
s[i] = i + 1;
psum[i] = i + 1;
}
for (int j = 1;j <= cnt && 1ll * i * pri[j] <= b;j ++){
vis[pri[j] * i] = 1;
if (i % pri[j] == 0){
psum[pri[j] * i] = psum[i] * pri[j] + 1;
s[pri[j] * i] = s[i] / psum[i] * psum[pri[j] * i];
break;
}
s[pri[j] * i] = s[i] * (pri[j] + 1);
psum[pri[j] * i] = pri[j] + 1;
}
}
for (int i = a;i <= b;i ++)
ans += abs(i * 2 - s[i]);
printf("%lld
",ans);
}
T5
题目描述
Daniel有一袋糖果和N张卡片。
每张卡片上都写有一个正整数Pi。丹尼尔在吃糖果的时候,想到了一个有趣的游戏。Daniel可以挑选两张卡片,将它们绑在一起,如果Daniel挑选第a张牌和第b张牌,那么Daniel会马上吃掉min(Pa%Pb,Pb%Pa)个糖果,其中x%y表示x除以y的余数。
Daniel每次会挑选两张卡片将它们绑在一起,最终,当他提起其中一张卡片时,所有其余的卡片也会被提起。他可以多次将同一张卡片和其他卡片绑在一起。Daniel要求你计算他至少要吃多少糖果。
输入
第一行输入包含一个整数N(1≤N≤1e5)。表示卡片的数量。
接下来N行每行包含一个正整数Pi(Pi≤1e7)。第i个整数Pi表示第i张卡片上的正整数。
输出
输出一个整数。表示Daniel至少要吃多少糖果。
样例
样例输入1
4
2
6
3
11
样例输出1
1
样例输入2
4
1
2
3
4
样例输出2
0
样例输入3
3
4
9
15
样例输出3
4
解题思路
一看也知道是一道最小生成树。然而数据太大了,用裸的最小生成树跑不仅会超时还会爆空间,可怕可怕。
正解其实就是最小生成树加优化。
首先,如果存在倍数关系,连边的花费就为0,我们可以缩点,但有一点要注意。不能够强行把这个点删去,我们把它放在一个集合中即可。强行删去会使得答案有误,其它点有可能与另一个点的倍数连边。列如3,11,22.
然后就是删边,我们要保存有意义的边。一些肯定用不上的边一定要删去。
我们定义一个数组q,q[i]则表示大于等于i的最小的数(原数列出现过)。
处理到一个点我们便可以枚举这一个值的倍数,至于那三个数的推导,给个链接但其实还有一个问题,那就是枚举倍数时这样加会有重复的边出现,我们仅仅需要存一个,就需要判断一下,看下一次塞进去的是不是与此相等。还有一点是,先处理判断一下q[p[i] + 1],然后再从2*p[i]开始枚举。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#define P 10000005
#include<cstdlib>
using namespace std;
struct node {
int u,v,w;
node (){};
node (int U,int V,int W){
u = U,v = V,w = W;
}
bool operator < (const node &a)const {
return w < a.w;
}
};
int n,p[P],cnt,fa[P],q[P],flag[P],maxn,a[P],k,n1;
bool vis[P];
vector <node>s;
void makeset(int x){
for (int i = 1;i <= x;i ++)
fa[i] = i;
}
int findset(int x){
if (fa[x] != x)
fa[x] = findset(fa[x]);
return fa[x];
}
int main(){
scanf ("%d",&n);
for (int i = 1;i <= n;i ++){
scanf ("%d",&p[i]);
maxn = max(p[i],maxn);
q[p[i]] = p[i];
flag[p[i]] = i;
}
makeset(maxn);
for (int i = maxn;i >= 0;i --)
if (!q[i])
q[i] = q[i + 1];
for (int i = 1;i <= n;i ++){
for (int j = p[i] * 2;j <= maxn;j += p[i]){
if (flag[j]){
int t1 = findset(p[i]);
int t2 = findset(j);
if (t1 != t2){
fa[t2] = t1;
k ++;
}
}
}
}
for (int i = 1;i <= n;i ++){
if (!vis[p[i]]){
vis[p[i]] = 1;
int t1 = findset(p[i]);
if (p[i] + 1 > maxn || (q[p[i] + 1] != q[p[i] + p[i]] && findset(q[p[i] + 1]) != t1))
s.push_back(node(p[i],q[p[i] + 1],q[p[i] + 1] % p[i]));
for (int j = p[i] * 2;j <= maxn;j += p[i]){
if (j + p[i] > maxn || (q[j] != q[j + p[i]] && findset(q[j]) != t1)){
s.push_back(node(p[i],q[j],q[j] % p[i]));
}
}
}
else
n1 ++;
}
sort(s.begin(),s.end());
long long mst = 0;
for (int i = 0;i < s.size() && k < n - n1 - 1;i ++){
int t1 = findset(s[i].u);
int t2 = findset(s[i].v);
if (t1 != t2){
if (t1 < t2)
fa[t2] = t1;
else
fa[t1] = t2;
mst += s[i].w;
k++;
}
}
printf("%lld
",mst);
}