什么是红黑树

编写不易，转载注明出处：https://www.cnblogs.com/lmh15054109/p/14239386.html

  在学习红黑树之前，需要先理解二叉查找树（Binary Search Tree）。

一、二叉查找树

二叉查找树（BST）特性

  1. 左子树上所有节点的值均小于或等于它的根节点的值。
  2. 右子树上所有节点的值均大于或等于他的根节点的值。
  3. 左、右子树也分别为二叉排序树。 

（1）查找

  查找一下节点值为10 的节点。

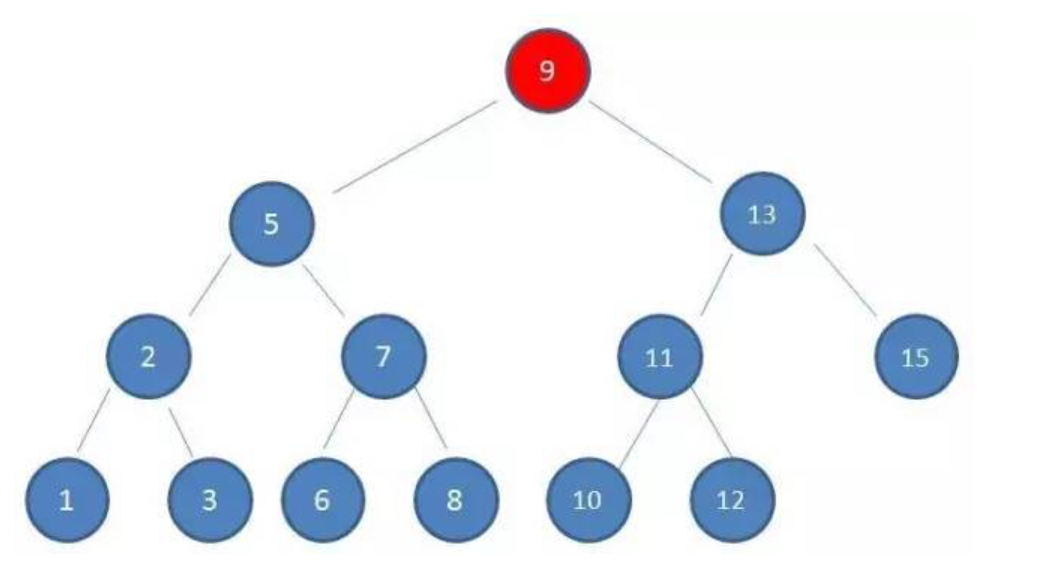
  1. 根节点为9,10>9，查看右孩子13。

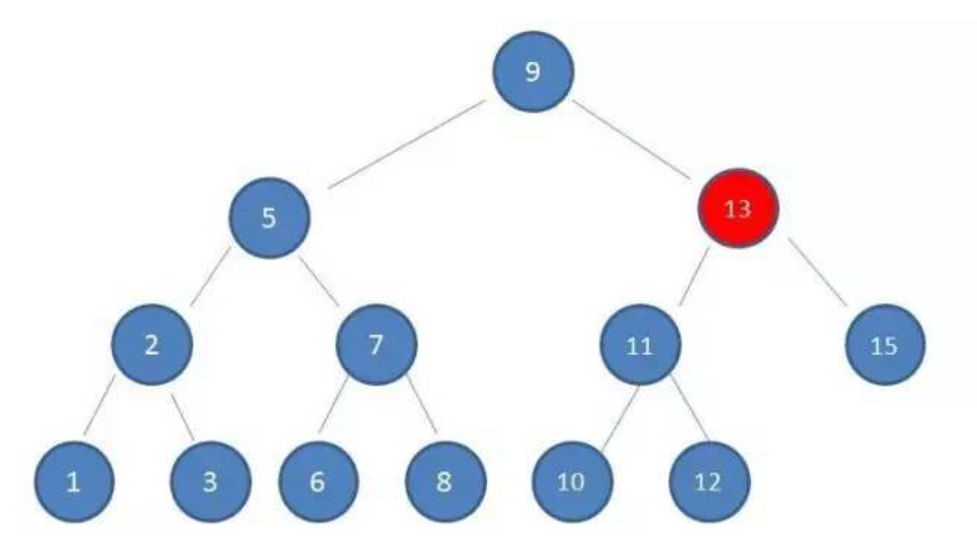
  2. 10<13 ,查看左孩子11。

3. 10 < 11 ，查看左孩子 10，刚好为需要查找的对象。

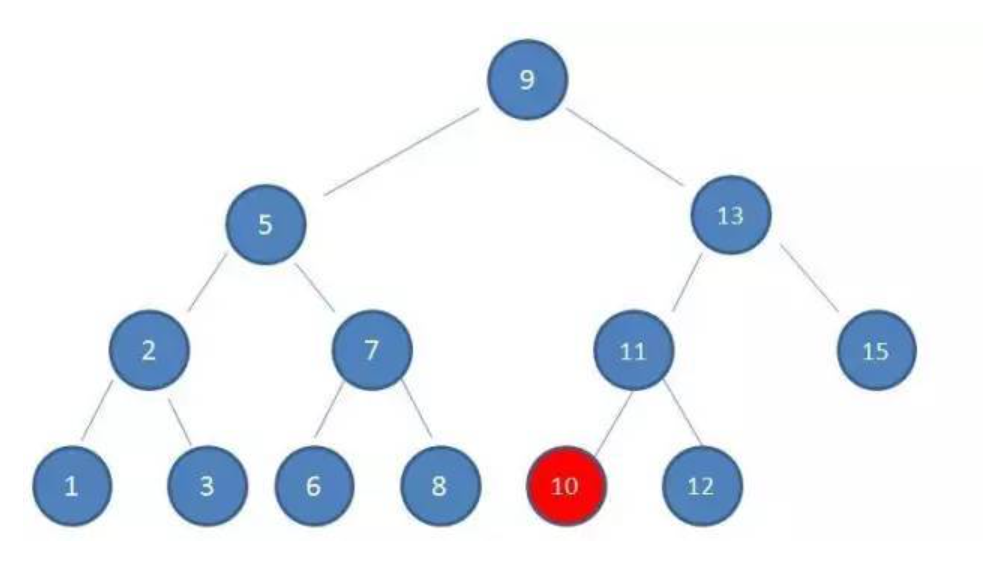
二叉查找树利用的正是二分查找的思想，查找所需的最大次数等同于二叉查找树的高度。

（2）插入

插入节点时，也使用类似的方法，通过一层一层的比较大小，找到新节点适合的位置，然后执行插入。

插入新节点的时候暴露出二叉查找树的缺陷。

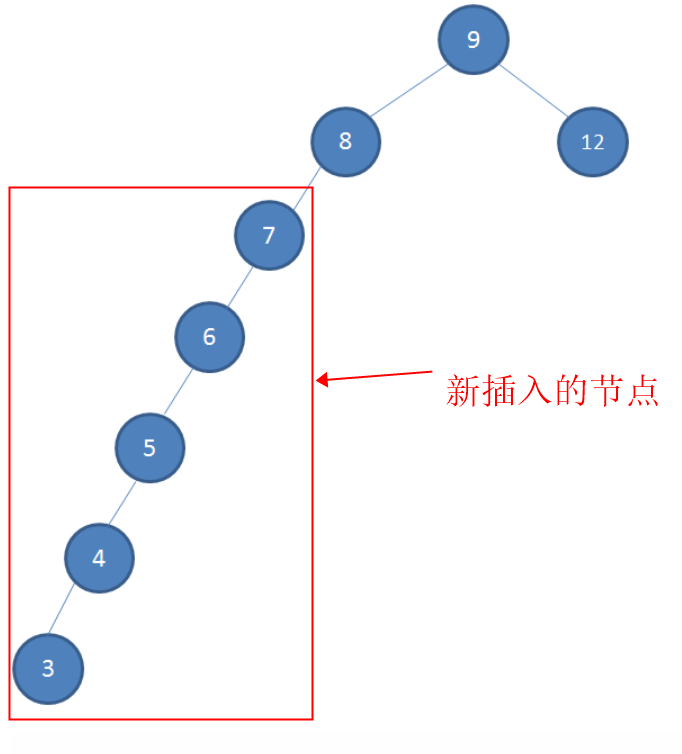
假设现在我们需要依照BST的特性，向初始只有三个节点，根节点为9，左孩子为8，右孩子为12的BST中依次插入7,6,5,4,3。其结果会入上图所示。

这样的形态虽然也符合二叉查找树的特性，但是查询的性能大打折扣，几乎变成线性的了。

红黑树就较好的解决了二叉查找树多次插入新节点而导致的不平衡。

二、红黑树

（1）红黑树的特性

红黑树（Red Black Tree）是一种自平衡的二叉查找树。出了符合BST的基本特性外，还具有其他特性。

规则：

1. 节点是红色或黑色的。
2. 根节点是黑色的。
3. 每个叶子节点都是黑色的空节点（NIL节点）。
4. 每个红色节点的两个子节点都是黑色的。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

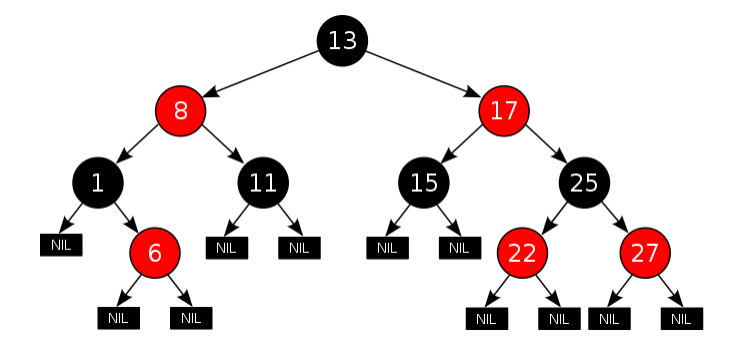
以上特性保证了红黑树的自平衡。红黑树从根到叶子的最长路径不会超过最短路径的两倍。

当插入或删除节点时，红黑树的规则有可能被打破。

例如：向原红黑树插入值为21的新节点：

其父节点是红色的，违反了规则4（每个红色节点的两个子节点都是黑色），我们需要进行必要的调整，使之重新符合红黑树的规则。

（2）红黑树的调整方式

红黑树的调整方式有两种，分别是：变色,旋转。其中旋转细分为：左旋转，右旋转。

变色：为了符合红黑树的规则，尝试把红色节点转变为黑色，或把黑色变为红色。

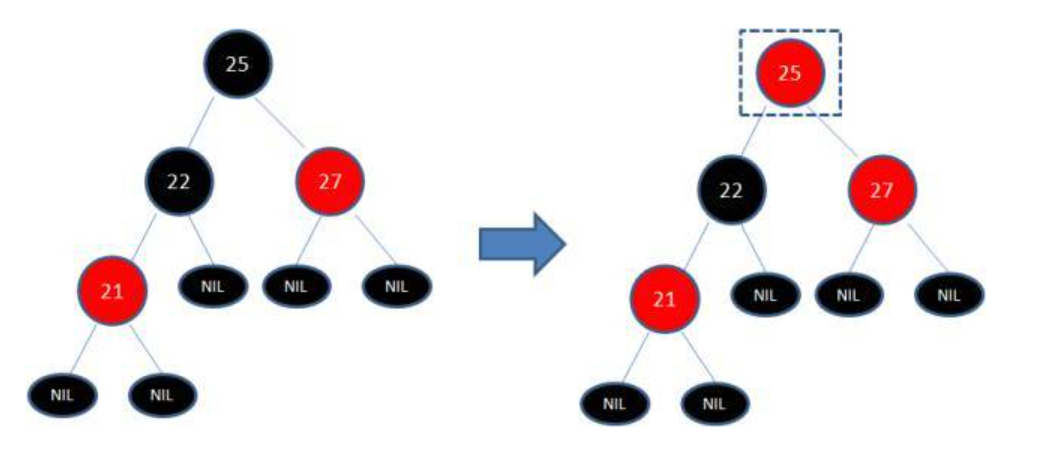
（1）由于21,22都为红色节点，违反了规则4（每个叶子节点到根节点的所有路径上不能有连续的红色节点），所以将22变成黑色。

（2）此时从25到其叶子节点违反了规则5，需要将25从黑色变成红色。

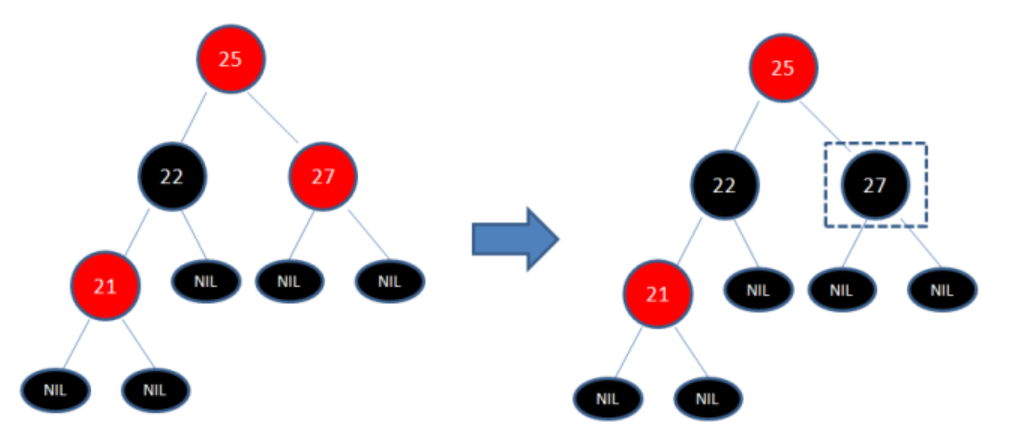
（3）此时，25、27形成了两个连续的红色节点，需要将27变为黑色。

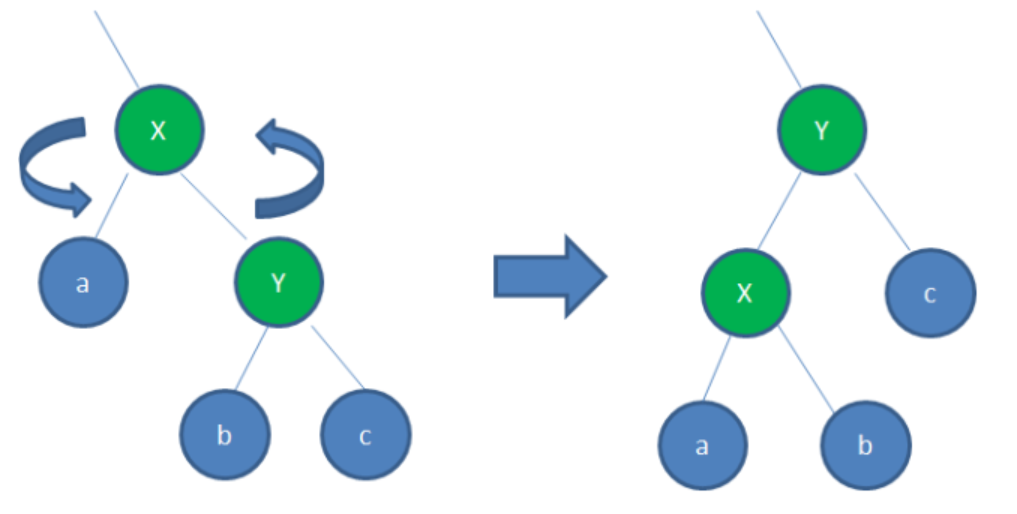
左旋转：逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为左孩子。

右旋转：顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为右孩子。

在上述插入节点21的例子中，经过变色形成了17,25两个连续红色节点的结果。如果将17变为黑色，将打破规则4，由于根节点能是黑色，所以根节点13不可能变成红色。

此时将13作为X，17作为Y进行左旋处理。

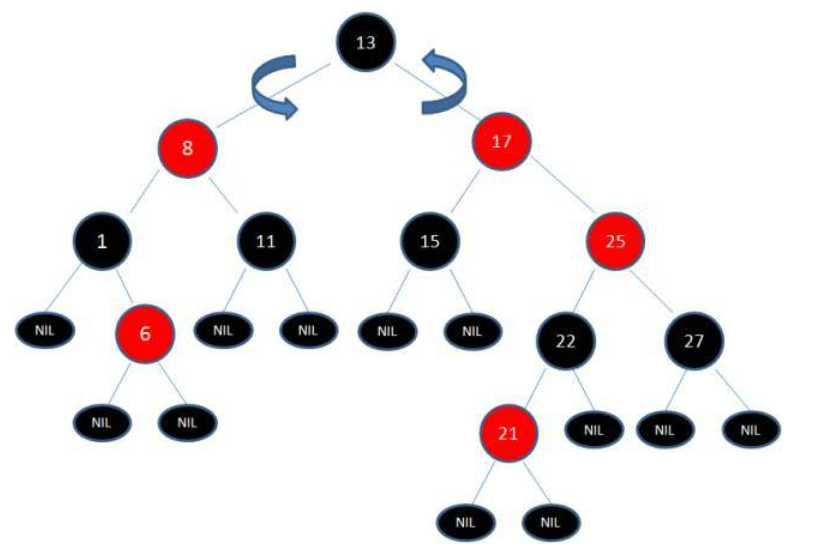
结果：

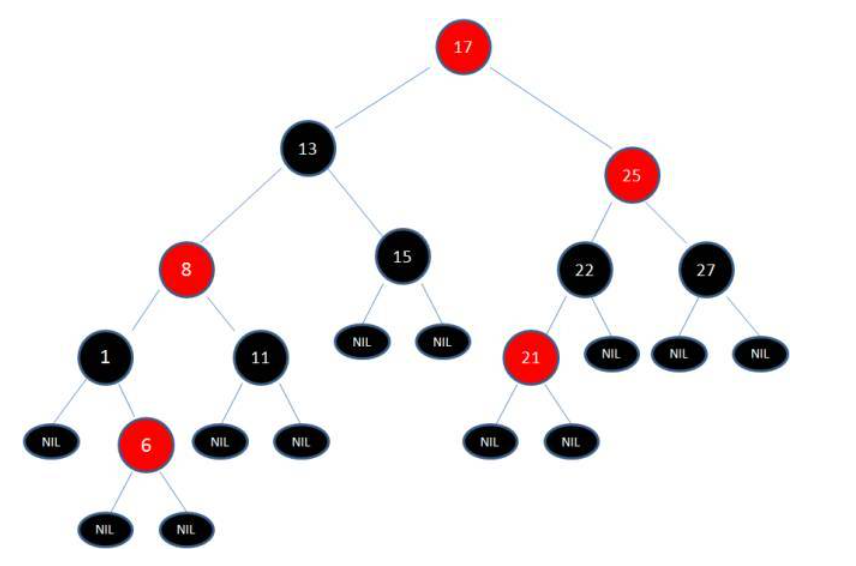
根据规则的2（根节点必须是黑色）进行变色，17变为黑色，根据规则5（从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点），13变为红色，8变为黑色，1,11变为红色，6变为黑色。

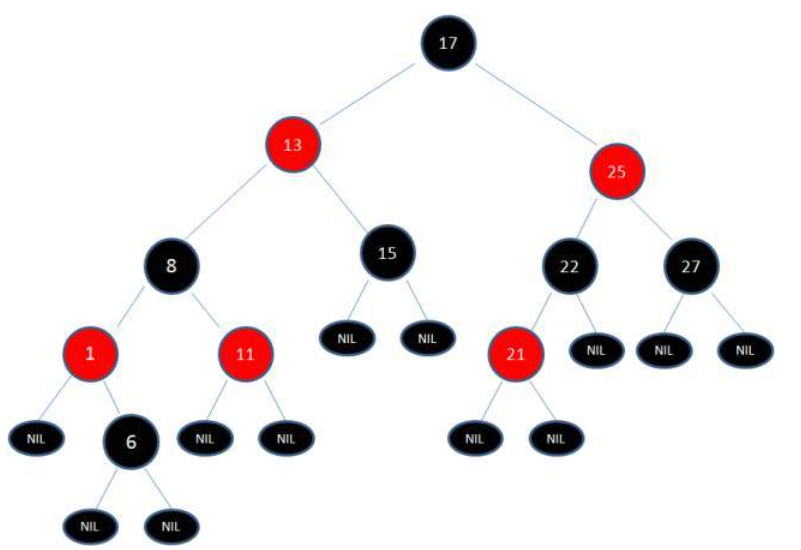
此时，红黑树调整貌似已经调整到位，其实不然。根据规则5可知从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点，从17到6到NIL节点的黑色节点个数是4，而其他路径的黑色个数是3，所以还需要继续处理。

我们将13看为X，8看为Y，进行右旋转操作。

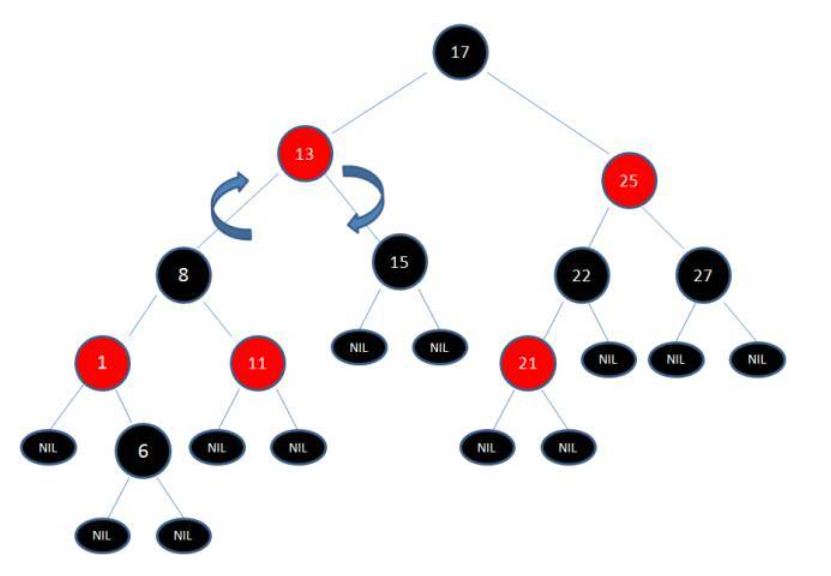
结果：

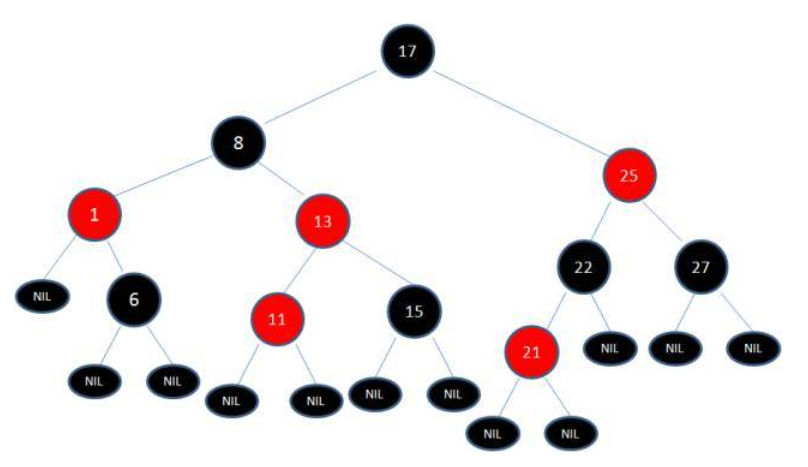
然后进行变色，最终：

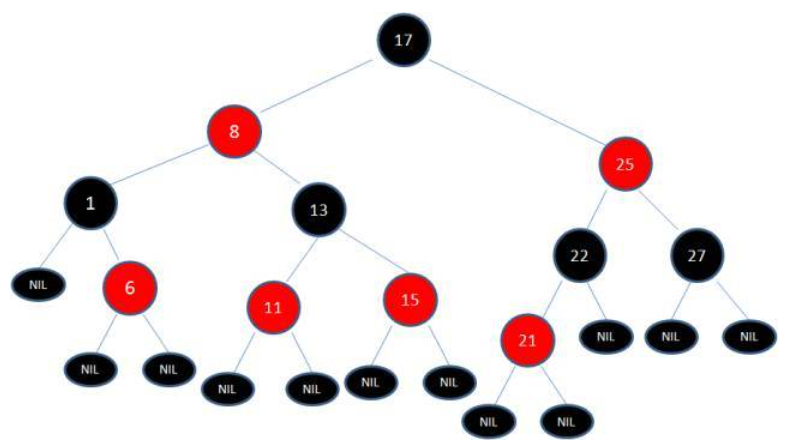
插入节点21到红黑树中的操作就完成，其中的步骤比较复杂，具体步骤为：

变色 ——>左旋转——>变色 ——>右旋转——>变色