一维前缀和: 即前i项的和
给定长度为n的序列a1,a2...an,则sum[i]=a1+...+ai=sum[i-1]+a[i]
for(i=1;i<=n;i++)
{
cin>>a[i];
a[i]+=a[i-1]; //直接累加
}
下面就来看一个简单的小应用:
问题:给定长度为n的序列a1,a2...an,(n<=1e5)给定q (q<=1e5)个询问[l,r],输出[l,r]的区间和。
输入:
10 5
1 2 3 4 5 5 4 3 2 1
1 6
3 8
1 10
5 5
1 3
输出:
20
24
30
5
5
本题可以用两种方法去做:
一、(肥肠简单粗暴)暴力计算每个询问[l,r]。O(q×n)
二、(肥肠实用)前缀和,输出每个询问[l,r]。O(n +q )
对比下两种方法的时间复杂度,是不是用前缀和快多了?
奉上前缀和代码——
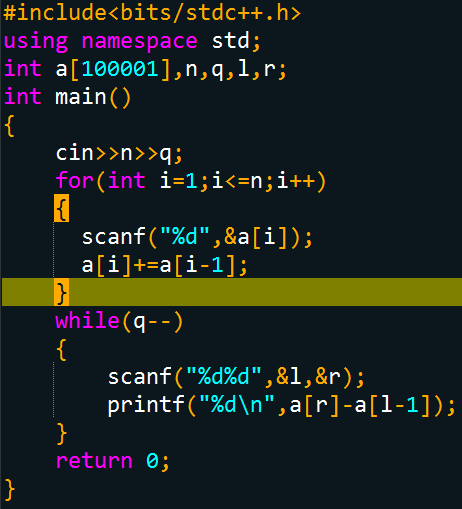
一维差分:区间一次修改求和
差分:每个元素与前一个元素的差值
如 a:1 2 3 4 5
则差分为b: 1 1 1 1 1 (b的前缀和即为a[i])
单点修改 a[i]+add:
若将a[1]+1, a: 1 3 3 4 5
则 b: 1 2 0 1 1 只会改变自己和后一个数(即b[i]+add , b[i+1]-add)
区间修改[l,r]增加add:
若将a数组[2,4]每个元素+1, a: 1 3 4 5 5
则 b: 1 2 1 1 0 只会改变b[l]和b[r]后一个数 ,即b[l]+add , b[r+1]-add
同样地,我们也来看一道例题:
问题:给定长度为n的序列a1,a2...an,(n<=1e5),初始都为0,接着m (m<=1e5)个操作 l,r,add表示给a数组[l,r]区间内的每个数加add,给定q (q<=1e5)个询问输出a[i]的值
输入:
105 5
1 6 1
3 8 2
1 10 1
5 5 5
1 3 3
2 4 3 6 10
输出:
5 4 7 4 1
just like lase one,看到本题之后依然会有两个想法:
一、暴力修改每个区间[l,r]。O(m×n)
二、差分修改每个区间[l,r]。O(1)
这差别有够明显吧☝☝☝
再次双手奉上差分代码——
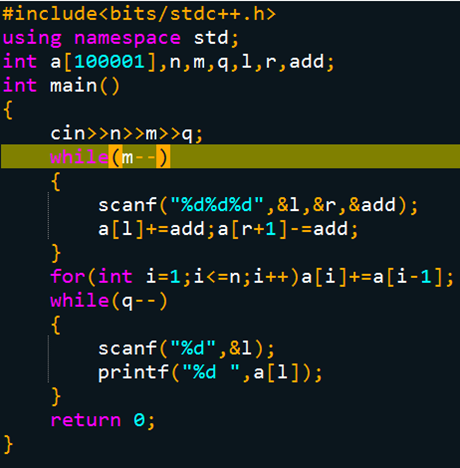
二维前缀和
这个主要是应用于在O(1)时间内求一个矩阵和。如给定一个矩阵s[i][j],sum[i][j]是矩阵s[1~i][1~j]的和。

则令sum[0][j]=sum[i][0]=0,矩形和等于黑矩形面积加上蓝矩形面积减去重叠矩形面积再加上红矩形面积。
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j];
又到了大展身手的时候!
问题:给定一个n*m大小的矩阵a,有q次询问,每次询问给定x1,y1,x2,y2四个数,求以(x1,y1)为左上角坐标和(x2,y2)为右下角坐标的子矩阵的所有元素和。注意仍然包含左上角和右下角的元素。

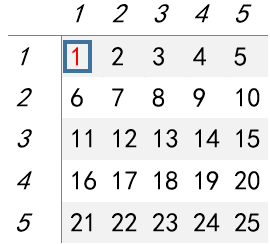
我们每次要求的答案就是红色圆圈所在的区域的值(注意,这里的x1,x2表示行,y1,y2表示列),对比上面这张图我们能够发现红色区域的值等于四个区域的值 减去(白色区域+黑色区域),再减去(白色区域+蓝色区域),最后因为白色区域被减了两次,我们需要再加回来。
所以ans=sum[x2][y2]-sum [x1-1][y2]-sum [x2][y1-1]+sum [x1-1][y1-1];
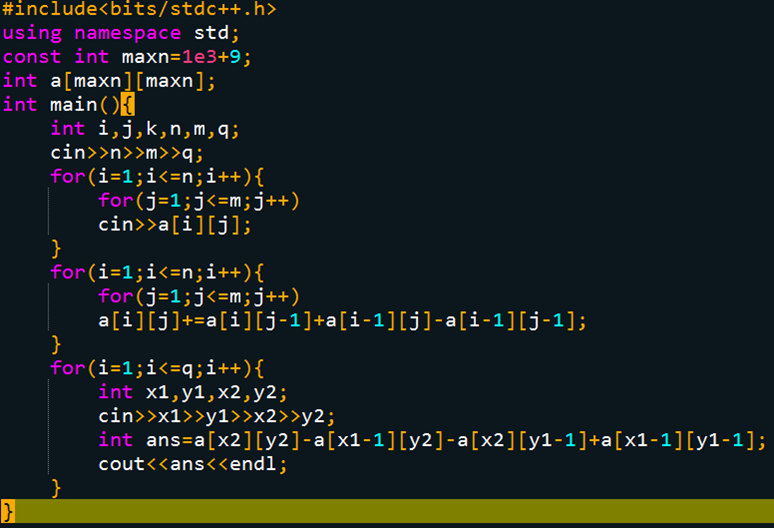
现在让我们回过头来看看贪心算法中的经典例题:
1224:最大子矩阵
详情请见☟☟☟
https://www.cnblogs.com/ljy-endl/p/11328369.html
那么二维怎么差分呢?我们先来看一道例题:
问题:一个n*n的矩阵,要求支持操作add(x1,y1,x2,y2,a),表示对于以(x1,y1)为左上角,(x2,y2)为右下角的矩形区域,每个元素都加上a。要求修改后的矩阵。
输入:
5 3
1 1 5 5 1
2 3 4 5 3
3 2 5 4 2
输出:
1 1 1 1 1
1 1 4 4 4
1 3 6 6 4
1 3 6 6 4
1 3 3 3 1
方法是和一维类似的,我们也是需要另开一个数组记录修改操作,最后求前缀和时统计修改操作,只是二维每一次操作需要记录4个位置,一维只需要记录2个位置。
for(int i=0;i<m;i++){//m是修改操作次数
int x1,y1,x2,y2,p;
cin>>x1>>y1>>x2>>y2>>p;
b[x1][y1]+=p;b[x2+1][y2+1]+=p;
b[x2+1][y1]-=p;b[x1][y2+1]-=p;
}
二维前缀和就是修改后的矩阵。
add(2 2 3 4 1)如下图☟☟☟
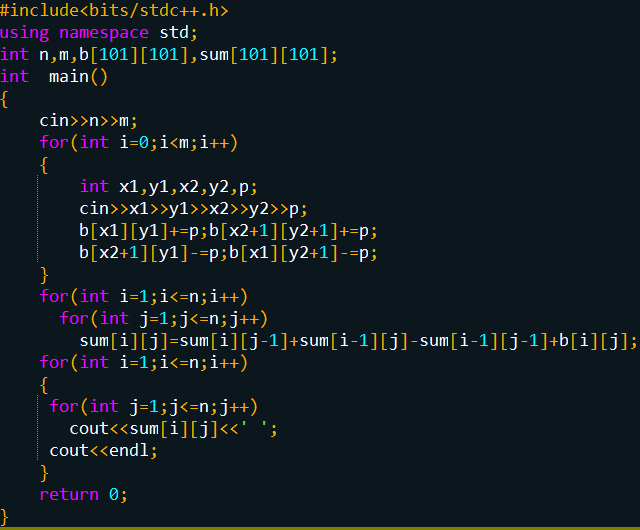
AC代码//撒花——
如果小可爱们想没事找事的话 勤奋的话,可以在洛谷找到相应的题目练习哟~;-)
1、 AT2412最大の和
题目传送门:https://www.luogu.org/problem/AT2412
题解传送门:https://www.cnblogs.com/ljy-endl/p/11330573.html
2、 P1115 最大子段和
题目传送门:https://www.luogu.org/problem/P1115
题解传送门:https://www.cnblogs.com/ljy-endl/p/11330658.html
3、 P3406海底高铁
题目传送门:https://www.luogu.org/problem/P3406
题解传送门:https://www.cnblogs.com/ljy-endl/p/11330735.html






