动态规划 , 零钱问题。

动态规划：核心思想，找到最优子结构，组合子问题构成原问题的解。

最重要的是，找到最优子结构，这是最难的部分

例题：我们有面值为1元3元5元的硬币若干枚，如何用最少的硬币凑够11元？

首先找到问题的子结构

1： 选择硬币作为子结构变量，

第一次选择只有1元硬币，求出构成11元硬币的方案集合A1，第二次选择有1,3元硬币，求出构成11元硬币的方案集合A2。第二次选择有1,3,5元硬币，求出构成11元硬币的方案集合A3。那么A1一定是A2的子集。A2一定是A3的子集。

从A3中选出使用最少硬币个数的方案就是最优方案。

步骤一：

首先建一个二维表X：

行代表能使用的硬币，用i表示int[] Coins={1,3,5}，列代表该列的总钱数，用j表示。

例如  X[1][5]  代表 硬币能使用coins[0],coins[1]  总钱数为5时，所需要的最小硬币个数。

只能使用1元硬币构成11元，求出个数，  

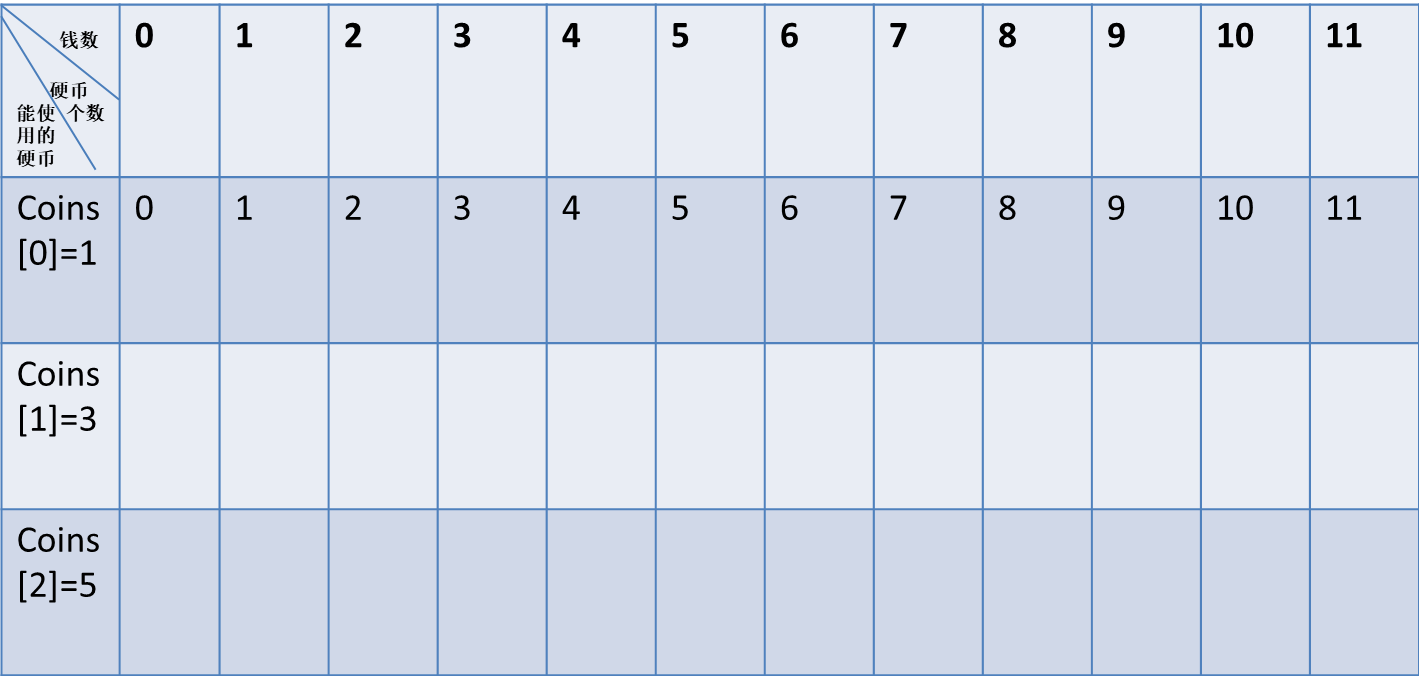
使用1,3元硬币构成11元，求出使用的硬币个数  。当选择1,3元硬币时，可以利用只用1元硬币求出的最优解。

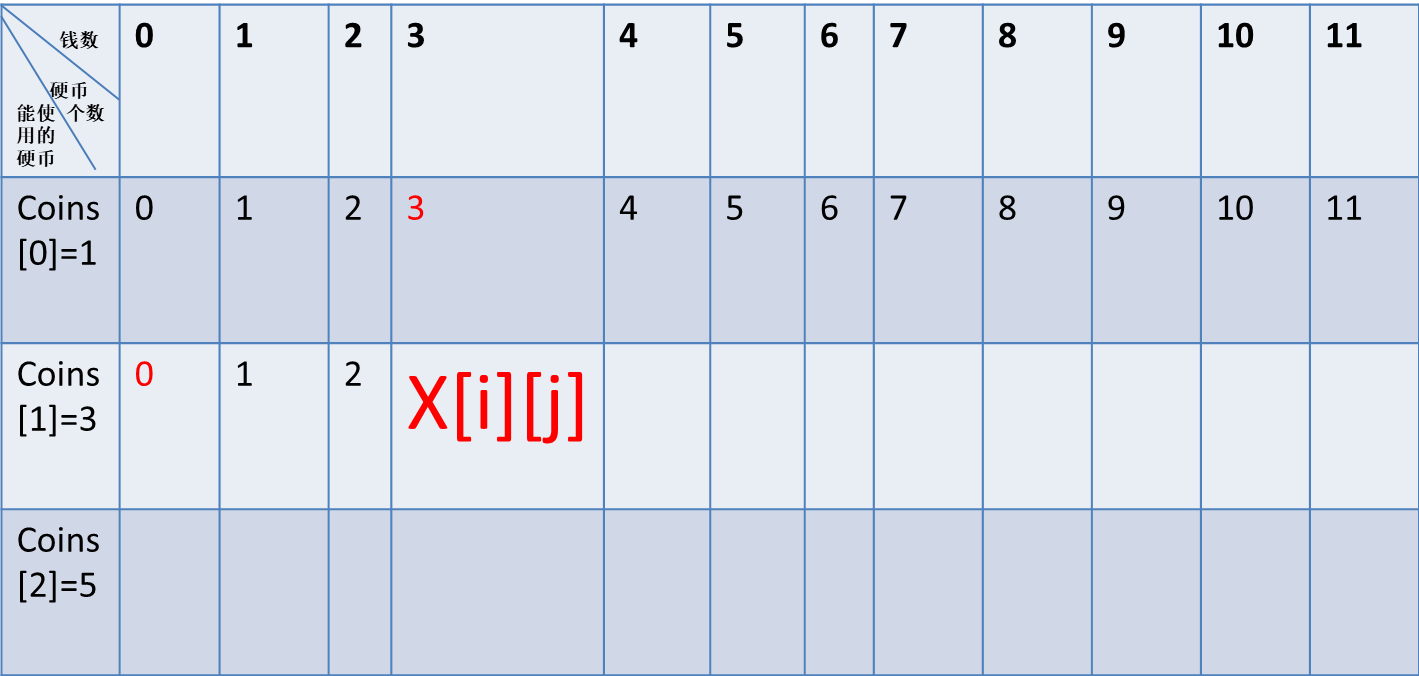
图中X[i][j]该如何求得，

a : 当总钱数小于新加入的硬币面值时，说明不能用新硬币。只能用之前的硬币求得的个数。

X[i][j]=X[i-1][j];

b:  当钱数大于等于新加入的硬币面值时，说明可以使用新硬币了

     b.1:如果使用新硬币，那么新硬币个数为1，  钱数为coins[i], 所以使用新硬币之后的个数为X[i][j]=X[i][j-coins[i]]+1;   

     b.2: 如果使用新硬币,  那么需要的硬币个数为 X[i][j]=X[i-1][j] 。 

     相比， 取较小的值。即为该钱数的情况下，使用的最小硬币个数。

X[i][j]=  min{X[i-1][j] ,X[i][j-coins[i]]+1}    

得到结果X[1][3]=min{X[1][0]+1 , X[0][3] } =X[1][0]+1 =1 ;

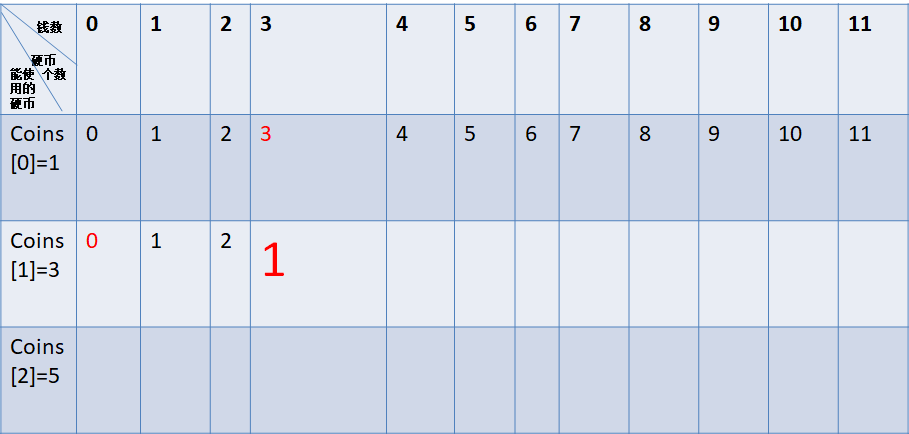
选择1,3,5元硬币构成11元硬币的，求出使用的硬币个数  

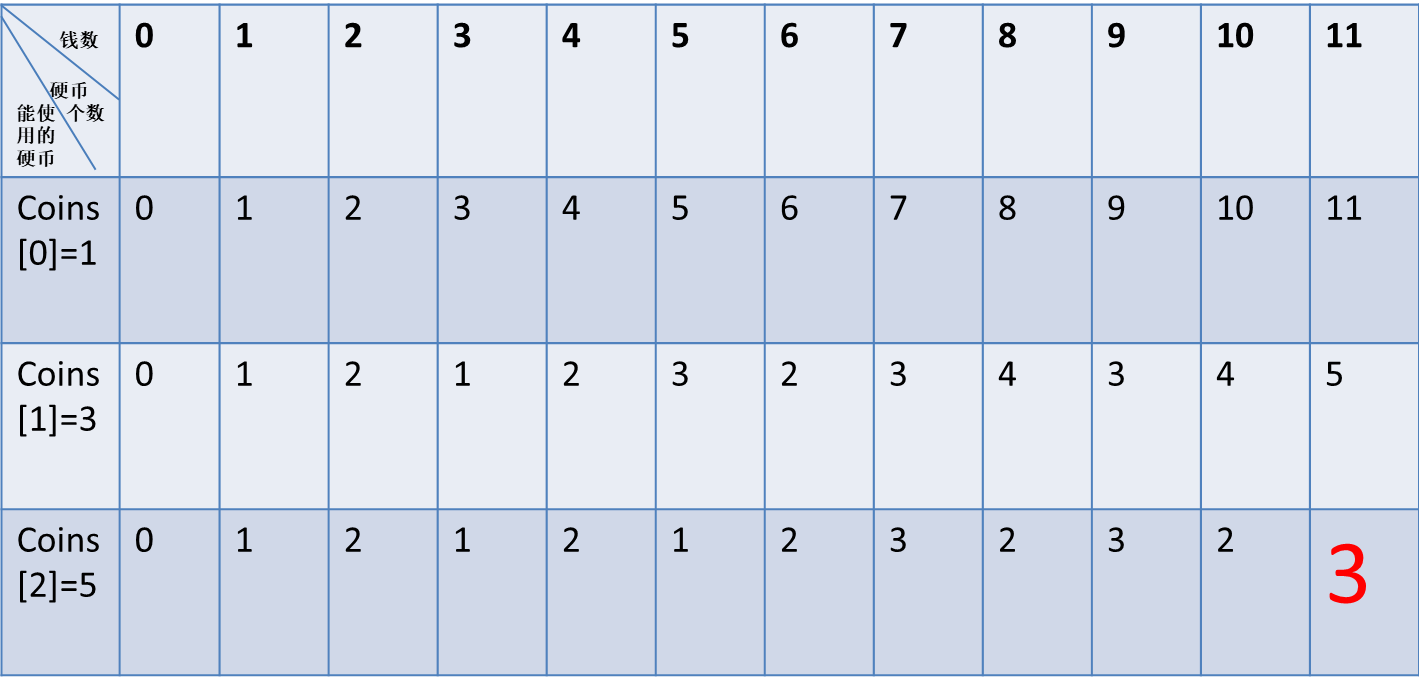
 最终的结果：使用的硬币为1,3,5。总钱数为11的值。

直接取出 X[2][11]即可。即为使用硬币的最小个数。

代码：

    public static void selectCoinAsVariable() {

        int[] coins = {1, 3, 5};

        int num=12;
        int[][] nums = new int[coins.length][num];

        for (int i = 0; i < num; i++) {
            nums[0][i]=i;
        }

        for (int i = 1; i < coins.length; i++) {
            for (int j = 1; j < num; j++) {
                if (j >= coins[i]) {
                    nums[i][j]=nums[i][j-coins[i]]+1>nums[i-1][j]?nums[i-1][j]:nums[i][j-coins[i]]+1;
                }else {
                    nums[i][j] = nums[i - 1][j];
                }
            }
        }

        System.out.println(nums[coins.length-1][num-1]);
    }

2：选择  总钱数作为 子结构变量。

      总钱数为6(6不为单个硬币的面额)的问题最优解，一定是从1,2,3,4,5的子问题的最优解中得出来的。

       初始化，当总钱数为单个硬币的面额时，最小个数一定为1。    创建一个数组number,  保存硬币个数。

     

从1开始，当总钱数为1时，因为有面额为1的硬币，那么个数为 number[1]=1 。

 总钱数为2时： 因为没有面额为2的硬币， 那么number[2] =number[1]+number[1]=2.

当总钱数为3时，因为有面额为3的硬币，那么个数为 number[3]=1 。  

当总钱数为4时,    因为没有面额为2的硬币，那么number[4]=min{number[3]+number[1]  ,   number[2]+number[2]} 。

...以此类推

当总钱数为11时：number[11]=min{number[1]+number[10]  ,   number[2]+number[9]  ,   number[3]+number[8]  ,   number[4]+number[7]   ,number[5]+number[6] }

最终，至少需要 3 个硬币构成 11 元钱number[11]。

 代码如下：

    public static void selectSumMoneyAsVariable() {

        int[] coins = {1, 3, 5};
        int num=12;

        int[] number = new int[num];
        for (int i = 0; i < coins.length; i++) {
            number[coins[i]] = 1;  //初始化，当总钱数为单个硬币的钱数时，最小个数为1。
        }

        for (int i = 2; i < num; i++) {
                int min=Integer.MAX_VALUE;
            for (int k = 1; k <=i/2 ; k++) {    //i-k的子问题一定比i的问题规模小。
                int value = number[i - k]+number[k];
                min=min>value?value:min;
            }
            if (number[i] !=1) {   //当i不是单个硬币的钱数时。
                number[i]=min;
            }
        }

        for (int i = 0; i < number.length; i++) {
            System.out.println(number[i]);
        }
    }