建议去看原文,下文只摘出了KMP过程且做了少许修改;https://www.cnblogs.com/SYCstudio/p/7194315.html
引入
- 首先我们来看一个例子,现在有两个字符串 A 和 B,问你在 A 中是否有 B,有几个?为了方便叙述,我们先给定两个字符串的值
- A = "abcaabababaa"
- B = "abab"
- 那么普通的匹配是怎么操作的呢?当然就是一位一位地比啦。(下面用蓝色表示已经匹配,黑色表示匹配失败)

- 但是我们发现这样匹配很浪费!为什么这么说呢,我们看到第 4 步:
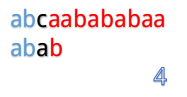
- 在第 4 步的时候,我们发现第 3 位上 c 与 a 不匹配,然后第 5 步的时候我们把 B 串向后移 1 位,再从第 1 个开始匹配

- 这里就有一个对已知信息很大的浪费,因为根据前面的匹配结果,我们知道 B 串的前 2 位是 ab,所以不管怎么移,都是不能和 b 匹配的,所以应该直接跳过对 A 串第 2 位的匹配,对于 A 串的第 3 位也是同理
- 再举一个例子

KMP算法
先摆出 2 个概念
前缀:指的是字符串的子串中从原串最前面开始的子串,如 abcdef 的前缀有:a,ab,abc,abcd,abcde
后缀:指的是字符串的子串中在原串结尾处结尾的子串,如 abcdef 的后缀有:f,ef,def,cdef,bcdef
- KMP算法引入了一个 F 数组(在很多文章中会称为next,但笔者更习惯用F,这更方便表达),F[i] 表示的是前 i 的字符组成的这个子串最长的相同前缀后缀的长度!
- 怎么理解呢?例如字符串
aababaaba的相同前缀后缀有a和aaba,那么其中最长的就是aaba - 那么,为了防止读者在接下来的内容中感到和笔者之前学习时同样的困惑,在这里先对下文做一些说明和约定
- 本文中,所有的字符串从 0 开始编号
- 本文中,F数组(即其他文章中的 next),F[i] 表示 0 ~ i 的字符串的最长相同前缀后缀的长度
F数组的运用
- 那么现在假设我们已经得到了 F 的所有值,我们如何利用 F数组 求解呢?
- 我们还是先给出一个例子(笔者用了好长时间才构造出这一个比较典型的例子啊)
- A = "abaabaabbabaaabaabbabaab"
- B = "abaabbabaab"
- 当然读者可以通过手动模拟得出只有一个地方匹配
- abaabaabbabaaabaabbabaab
- 那么我们根据手动模拟,同样可以计算出各个 F 的值

- 我们再用 i 表示当前 A 串要匹配的位置(即还未匹配),j 表示当前 B 串匹配的位置(同样也是还未匹配),补充一下,若 i>0 则说明 i-1 是已经匹配的啦( j 同理)
举例说明匹配过程
- 首先我们还是从 0 开始匹配:
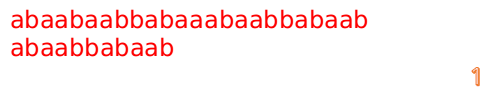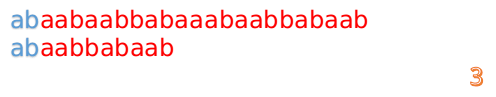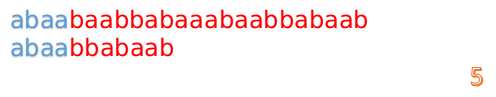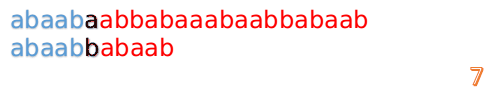
- 此时,我们发现,A 的第 5 位和 B 的第 5 位不匹配(注意从0开始编号),此时i=5,j=5,那么我们看 F[j-1] 的值:
F[5-1] = 2; - 这说明我们接下来的匹配只要从 B 串第 2 位开始(也就是第 3 个字符)匹配,因为前两位已经是匹配的啦(想象成先前已经移动 {B 串}, 让它和 { A 串的前 i - 1 个字符构成的串} 的后缀对齐了),具体请看图:


- 然后再接着匹配:
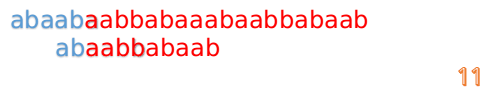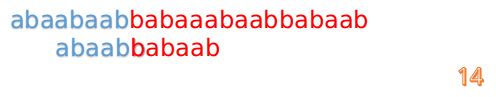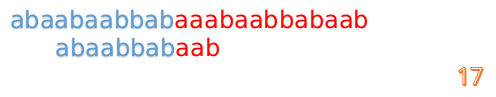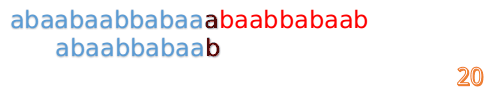
- 我们又发现, A 串的第 13 位和 B 串的第 10 位不匹配,此时 i=13,j=10,那么我们看 F[j-1] 的值:
F[10-1] = 4 - 这说明 B 串的 0~3 位是与当前 (i-4)~(i-1) 是匹配的,我们就不需要重新再匹配这部分了,把 B 串向后移,从B串的第 4 位开始匹配:
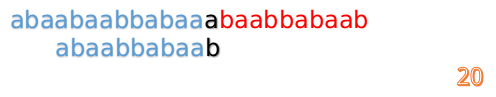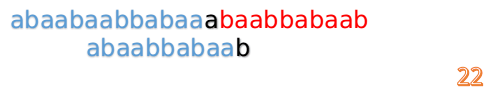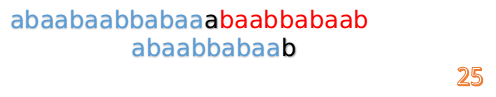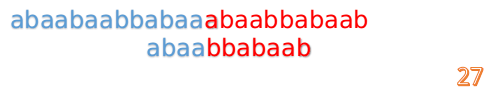

- 这时我们发现 A 串的第 13 位和 B 串的第 4 位依然不匹配

- 此时i=13,j=4,那么我们看 F[j-1] 的值:
F[4-1] = 1 - 这说明 B 串的第 0 位是与当前 i-1 位匹配的,所以我们直接从 B 串的第 1 位继续匹配:

- 但此时 B 串的第 1 位与 A 串的第 13 位依然不匹配
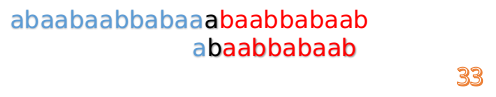
- 此时,i=13,j=1,所以我们看一看 F[j-1] 的值:
F[1-1] = 0 - 好吧,这说明已经没有相同的前后缀了,直接把 B 串向后移 1 位,直到发现 B 串的第 0 位与 A 串的第 i 位可以匹配(在这个例子中,i = 13)

- 再重复上面的匹配过程,我们发现,匹配成功了!

这就是KMP算法的全过程

另外强调一点,当我们将 B 串向后移的过程其实就是 i++ ;而当我们不动 B,而是匹配的时候,就是i++,j++,这在后面的代码中会出现,这里先做一个说明