1. 引入
给你一个数列 {7, 3, 10, 12, 5, 1, 9},要求能够高效的完成对数据的查询和添加。
1. 使用数组
- 数组未排序
- 优点:直接在数组尾部添加,速度快
- 缺点:查找速度慢
- 数组排序
- 优点:可以使用二分查找,查找速度快
- 缺点:为了保证数组有序,在添加新数据时,找到插入位置后,后面的数据需整体移动,速度慢
2. 使用链表
不管链表是否有序,查找速度都慢,添加数据速度比数组快,不需要数据整体移动
3. 使用二叉排序树
2. BST 介绍
- 二叉排序/搜索树(Binary Sort/Search Tree,简称 BST),对于二叉排序树的任何一个非叶子结点,要求:
- 左子结点的值比当前结点的值小
- 右子结点的值比当前结点的值大
- 特别说明:如果有相同的值,可以将该节点放在左子结点或右子结点
- 比如针对前面的数据 {7, 3, 10, 12, 5, 1, 9},对应的二叉排序树为:
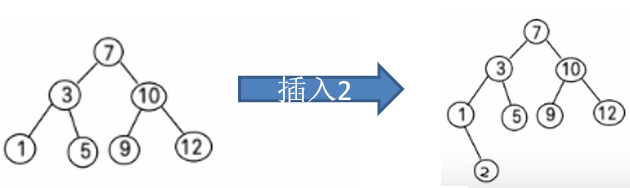
3. BST 删除结点
3.1 删除叶子结点
- 找到待删除的结点 targetNode
- 找到 targetNode 的父结点
- 确定 targetNode 是 parent 的左子结点,还是右子结点
- 根据 step3 来进行删除
3.2 删除只有一颗子树的结点
- 找到待删除的结点 targetNode
- 找到 targetNode 的父结点 parent
- 确定 targetNode 是父结点的左子结点还是右子结点
- 确定 targetNode 的子结点是左子结点还是右子结点
- 分 4 种情况
// 父之左 & 子在左 parent.left = targetNode.left; // 父之左 & 子在右 parent.left = targetNode.right; // 父之右 & 子在左 parent.right = targetNode.left; // 父之右 & 子在右 parent.right = targetNode.right;
3.3 删除有两颗子树的结点
- 找到待删除的结点 targetNode
- 找到 targetNode 的父结点 parent
- 从 targetNode 的右(左)子树中找出 value 最小(大)的结点
- 用一个临时变量 temp 来保存该最小(大)结点的 value
- 删除该最小(大)结点,并让 targetNode.value = temp // 可以理解为:用 targetNode 的右(左)子树中的最小(大)结点来替代 targetNode
4. 代码实现
class BinarySortTree {
Node root;
public void add(Node node) {
if (root == null) root = node;
else root.add(node);
}
public void infixOrder() {
if (root != null) root.infixOrder();
else System.out.println("空树");
System.out.println();
}
public Node searchNode(int value) {
if (root == null) return null;
else return root.searchNode(value);
}
public Node searchParent(int value) {
if (root == null || value == root.value) return null;
else return root.searchParent(value);
}
/**
* 删除node的最小value子结点, 并返回该最小结点的value
* @param node 二叉排序树的根结点
* @return 以node为根结点的二叉排序树的最小值
*/
public int delTreeMinNode(Node node) {
Node target = node;
// 循环的查找左子结点
while (target.left != null) target = target.left;
// 这时, target就指向了最小结点
delNode(target.value);
return target.value;
}
/**
* 删除node的最大value子结点, 并返回该最大结点的value
* @param node 二叉排序树的根结点
* @return 以node为根结点的二叉排序树的最小值
*/
public int delTreeMaxNode(Node node) {
Node target = node;
// 循环的查找右子结点
while (target.right != null) target = target.right;
// 这时, target就指向了最小结点
delNode(target.value);
return target.value;
}
public void delNode(int value) {
if (root == null) return;
// 1. 找到待删除结点
Node targetNode = searchNode(value);
// a. 待删除结点不存在
if (targetNode == null) return;
// b. 存在, 是根结点,且这颗树只有这 1 个结点
if (root.left == null && root.right == null) {
root = null;
return;
}
// 2. 找待删除结点的父结点
Node parent = searchParent(value);
// 3. 删除
if (targetNode.left == null && targetNode.right == null) { // 3.1 叶子结点
// 判断 targetNode 是 parent 的左子结点还是右子结点
if (parent.left != null && parent.left.value == value)
parent.left = null;
else if (parent.right != null && parent.right.value == value)
parent.right = null;
} else if (targetNode.left != null && targetNode.right != null) { // 3.2 双子结点
// a. 删除 targetNode 的右子树中 value 最小的结点, 并将其 value 赋值给 targetNode
targetNode.value = delTreeMinNode(targetNode.right);
// b. 删除 targetNode 的左子树中 value 最大的结点, 并将其 value 赋值给 targetNode
// targetNode.value = delTreeMaxNode(targetNode.left);
} else { // 3.3 单子结点
if (parent.left != null && parent.left.value == value) { // 父之左
if (targetNode.left != null) { // 子在左
parent.left = targetNode.left;
} else { // 子在右
parent.left = targetNode.right;
}
} else { // 父之右
if (targetNode.left != null) { // 子在左
parent.right = targetNode.left;
} else { // 子在右
parent.right = targetNode.right;
}
}
}
}
}
class Node {
int value;
Node left;
Node right;
public Node(int value) {
super();
this.value = value;
}
// 查找结点
public Node searchNode(int value) {
if (value == this.value) {
return this;
} else if(value < this.value) {
if (this.left != null) return this.left.searchNode(value);
else return null;
} else {
if (this.right != null) return this.right.searchNode(value);
else return null;
}
}
/**
* 查找某个结点的父结点
* @param value 子结点的value
* @return 父结点
*/
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value)
|| (this.right != null && this.right.value == value)) {
return this;
} else {
if (value < this.value && this.left != null)
return this.left.searchParent(value);
else if (value > this.value && this.right != null)
return this.right.searchParent(value);
else
return null;
}
}
// (递归)添加结点
public void add(Node node) {
if (node == null) return;
// 判断node的value和当前子树根结点的value的大小关系
if (node.value < this.value) {
if (this.left != null) his.left.add(node);
else this.left = node;
} else {
if (this.right != null) this.right.add(node);
else this.right = node;
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) this.left.infixOrder();
System.out.print(this + " ");
if (this.right != null) this.right.infixOrder();
}
@Override
public String toString() {
return "[value=" + value + "]";
}
}