bzoj3505[CQOI2014]数三角形

题意:给你一张n*m(n,m<=1000)的网格图,问有多少个顶点在格点上的三角形（共线不算）.

首先补集转化,不考虑共线的方案是C(n*m,3),减去共线方案数即可.

对于共线方案数的统计，首先可以考虑O(n^4)暴力枚举两个端点(x1,y1)(x2,y2),中间的点有gcd(x2-x1,y2-y1)-1个.然后发现可以只O(n^2)枚举(x2-x1)和(y2-y1)的值,数一数对应的情况有多少个,相当于在网格图内平移一个长(x2-x1)宽(y2-y1)的矩形,能摆在多少个不同的位置，那么就是(n-(x2-x1)+1)*(m-(y2-y1)+1)种.

我写了一发DP，略有不同，不过思想是相通的。

记f[i][j]为点(i,j)为左上角时的重复方案数，包括斜向的和水平垂直的.例如f[1][1]=0,f[1][2]=0,f[1][3]=1,f[2][2]=0,f[3][3]=3

(题目里给的n,m是“长度”，也就是说输入n时一条边有n+1个点,我这里状态定义的坐标略有不同,f[1][1]是一个孤立的点,f[2][2]是四个点组成的正方形)

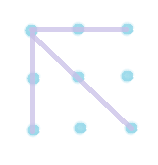
  (这是f[3][3]=3)

转移的时候,考虑从f[i-1][j]转移到f[i][j].

实际上，可以认为f[i][j]是在f[i-1][j]的图形右侧加了一列,左上角没有动

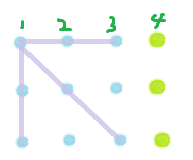
（从f[3][3]变到f[4][3],可以看到增加了图中点(1,2,4)(1,3,4)的共线情况）

一个结论:点(i,j)和点(i+dx,j+dy)的连线上除了端点,有gcd(dx,dy)-1个整点. 因为每次是增加整整一列，暴力转移是O(n^3)的.但是一起考虑i相同的所有状态,会发现它们转移时有大量重复计算。

例如:f[4][3]=f[3][3]+[gcd(3,0)-1]+[gcd(3,1)-1]+[gcd(3,2)-1]

        f[4][4]=f[3][4]+[gcd(3,0)-1]+[gcd(3,1)-1]+[gcd(3,2)-1]+[gcd(3,3)-1]因此可以记录后边那个gcd-1的和,每个状态的转移是O(1)的. 注意这里只算了向右下方倾斜的,但向左向右倾斜都可以，所以根据对称要乘2.处理向左/向右倾斜的时候我把水平和垂直的情况算了两次,最后还要单独处理一下.

(f数组可以不用long long. N^2对数的gcd可以用辗转相减递推预处理)

#include<cstdio>
typedef long long ll;
const int maxn=1005;
int g[maxn][maxn],f[maxn][maxn];
ll m,n;
void init(){
    for(int i=0;i<maxn;++i)g[i][i]=g[i][0]=g[0][i]=i;
    for(int i=1;i<maxn;++i){
        for(int j=1;j<=i;++j){
            g[j][i]=g[i][j]=g[j][i-j];
        }
    }
}
int main(){
    scanf("%lld%lld",&m,&n);m++;n++;
    init();
    ll ans=(m*n)*(m*n-1)*(m*n-2)/6;
    for(int i=1;i<=n;++i){
        int tmp=0;
        for(int j=1;j<=m;++j){
            //blablabla
            if(g[j-1][i-1])tmp+=g[j-1][i-1]-1;
            f[i][j]=f[i-1][j]+tmp;
            ans-=f[i][j]*2;
        }
    }    
    if(n>=3)ans+=m*(n)*(n-1)*(n-2)/6;
    if(m>=3)ans+=n*(m)*(m-1)*(m-2)/6;
    printf("%lld
",ans);
    return 0;
}