AcWing 106. 动态中位数

题目传送门

一、算法分析

添加一个元素时： 原则：构造一个漏斗形式的两个对顶堆：

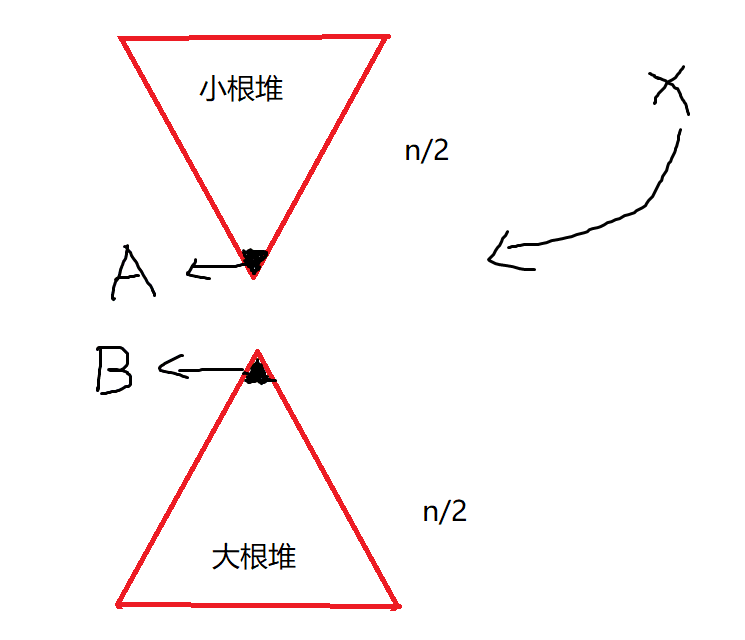
大的元素往小根堆里面放, 小的元素往大根堆里面放

保证\(A\)和\(B\)的值可以取到中位数，并且 规定小根堆比大根堆最多多一个 :
假想我们已经处在一个符合要求的场景下，现在新来一个元素\(x\):

• 若小根堆为空或者\(x >= A\)，则插入到小根堆\(up\)中，否则插入到大根堆中。

• 维护大根堆和小根堆的数量关系：小根堆比大根堆最多多一个:

  • 若\(up.size() > down.size() + 1\)，将小根堆的堆顶元素转移到大根堆中

  • 若\(down.size() > up.size()\)，将大根堆的堆顶元素转移到小根堆中

获取中位数

若总体数量为奇数时，中位数为\(A\)

若总体数量为偶数时，中位数为\((A + B)/2\)

二、实现代码

#include <bits/stdc++.h>
using namespace std;
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n, m;
        scanf("%d%d", &m, &n);
        printf("%d %d\n", m, (n + 1) / 2);

        priority_queue<int> down;                          //默认大顶堆
        priority_queue<int, vector<int>, greater<int>> up; //小顶堆
        //形成一个对顶堆，又称漏斗堆

        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            int x;
            scanf("%d", &x);

            if (down.empty() || x <= down.top())
                down.push(x);
            else
                up.push(x);

            //保证两个堆之间的数字个数为up mid down的关系，即len(up)+1=len(down)
            if (down.size() > up.size() + 1) up.push(down.top()), down.pop();
            if (up.size() > down.size()) down.push(up.top()), up.pop();
            //奇数才输出
            if (i % 2) {
                printf("%d ", down.top());
                if (++cnt % 10 == 0) puts(""); //题目要求十个一换行
            }
        }
        //最后不足10个，也需要输出一个的换行
        if (cnt % 10) puts("");
    }
    return 0;
}