AcWing 1148 秘密的牛奶运输

题目传送门

一、次小生成树

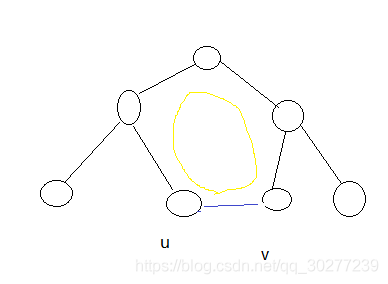
蓝色边为新添加的边，黑色边为最小生成树

概念

最小生成树
生成树是指包含图中所有节点的一棵树，而最小生成树则指一棵所有边的权值之和最小的生成树。

结论

连接\(uv\)后，生成了一个环，此环中\(uv\)的距离\(w\)就是最大值
证明：设最小生成树的边权之和是\(sum\), \(uv\)的距离是\(w\),那么在连接通\(uv\)这两个点后，必然形成了一个环，如图所示
这个环中，每条边的长度\(w_i\)必然小于等于\(w\)。为什么呢?

因为如果这个环中某条边的长度是大于\(w\)的，那么我们可以把这条小边\(w_i\)删除掉，就可以得到一个新的生成树，而这个新的生成树，由于去掉了\(w_i\),又加上了\(w\),所以完成操作后最小生成树的长度为\(sum-w_i+w\),那么新的生成树的边权和就将变小，这与最初就是最小生成树矛盾，问题得证。

推论

次小生成树与最小生成树差的只是一条边。
证明：我们先建出一棵最小生成树，满足使用的边都是最小的，剩下的边（称为非树边）一定没有树边优。如果我们加入一条非树边，删除最小生成树中的一条边，次小生成树一定是包括在以这种方法建出的树中的（倘若删两条树边加两条非树边，则肯定没有删一条加一条优，绝不是次小生成树）

目标

得到一个严格次小生成树

思路

严格次小生成树，这个严格很讨厌。因为有可能我们在枚举到一个非树边去替换最小生成树中（可以和这条非树边组成环的那些边）的某条边时，可能与某条边是一样长的，之所以会产生这样的情况，是因为本来最小生成树也不是唯一的。

但出现这样的情况时，我们还不能认为这样就continue,而是需要去替换这个环中次长边，也可以拿到一个备选的次小生成树。

求法

1、利用\(Kruskal\)算法，求出最小生成树，计算出\(sum\)值，同时，需要把最小生成树单独建图，下面会在最小生成树中计算每个点到另一个点的最长距离和次长距离。
2、在最小生成树中，计算出任意两点间的最短距离。
3、枚举所有非树边,尝试去替换\(u\)到\(v\)的在最小生成树路径上的最大边或次大边。
4、步骤\(3\)中所有\(sum-w_i+w\)取最小值就是次小生成树的边权和。

二、实现代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 510, M = 10010;
int n, m;
typedef pair<int, int> PII;
//结构体
struct Edge {
    int a, b, w;
    bool flag; //是不是最小生成树中的边
    bool operator<(const Edge &t) const {
        return w < t.w;
    }
} edge[M];

PII dist[N][N]; //从i出发，到达j最短距离和次短距离
LL sum;         //最小生成树的边权和
//邻接表
int h[N], e[M], w[M], ne[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
//并查集
int p[N];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
//在一棵树中求从u节点出发路径中最大的边权和次大的边权
void dfs(int u, int fa, int m1, int m2, PII d[]) {
    d[u].first = m1, d[u].second = m2;       //收集结果：最大值和次大值
    for (int i = h[u]; ~i; i = ne[i]) {      //枚举u的每一条出边
        int j = e[i];                        // j为u的对边节点
        if (j != fa) {                       //不走回头路
            //这里需要拷贝出来，因为从同一个位置,安排多个哨兵出发携带的信息需要是一样的
            int t1 = m1, t2 = m2;
            if (w[i] > t1)
                t2 = t1, t1 = w[i];          //更新最大值、次大值
            else if (w[i] < t1 && w[i] > t2) //严格次大值
                t2 = w[i];                   //更新次大值
            // 继续传递，是为了记录结果到数组d中，引用传递
            dfs(j, u, t1, t2, d);
        }
    }
}

int main() {
    cin >> n >> m;
    //初始化邻接表
    memset(h, -1, sizeof h);
    // Kruskal
    for (int i = 0; i < m; i++)
        cin >> edge[i].a >> edge[i].b >> edge[i].w;
    //按边权由小到大排序
    sort(edge, edge + m);
    //并查集初始化
    for (int i = 1; i <= n; i++) p[i] = i;
    //最小生成树
    for (int i = 0; i < m; i++) {
        int a = edge[i].a, b = edge[i].b, w = edge[i].w;
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            p[pa] = pb;
            //最小生成树的边权和
            sum += w;
            //最小生成树建图,无向图
            //为求最小生成树中任意两点间的路径中最大距离、次大距离做准备
            add(a, b, w), add(b, a, w);
            //标识此边为最小生成树中的边,后面需要枚举每条不在最小生成树中的边
            //尝试加入到最小生成树中，替换掉最小生成树中的某一条边，来获取到次小生成树
            edge[i].flag = true;
        }
    }

    // dist1[i][j]和dist2[i][j]
    //计算i节点到最小生成树中j节点路径中的最长和次长距离是多少
    for (int i = 1; i <= n; i++) //这一步是有优化空间的
        dfs(i, -1, -1e9, -1e9, dist[i]);

    LL res = 1e18; //预求最小值，先设最大值
    //枚举所有不在最小生成树中的边,尝试加入u~v的这条直边
    for (int i = 0; i < m; i++)
        if (!edge[i].flag) {
            int a = edge[i].a, b = edge[i].b, w = edge[i].w;
            LL t;
            if (w > dist[a][b].first)
                t = sum + w - dist[a][b].first; //替换最大边
            else if (w > dist[a][b].second)     //替换次大边
                t = sum + w - dist[a][b].second;
            //次小生成树的边权和
            res = min(res, t);
        }
    //输出
    printf("%lld\n", res);
    return 0;
}