转载自:https://blog.csdn.net/zwx19921215/article/details/84303646
数组的定义
数组是由n(n>1)个具有相同数据类型的数据元素a1...an组成的有序序列,且该序列必须存储在一块地址连续的存储单元中。
1.数组中的数组元素就有相同的数据类型
2.数组是一种随机存取结构,给定一组下标就可以访问与其对应的数据元素。
3.数组中的数据元素个数是固定的。
行向量的一位数组形式

列向量的一位数组形式

数组的两种顺序存储方式
1.行优先顺序(Row Major Order):将数组元素按行排列,第i+1个行向量紧接着第i个行向量后面。对于二维数组,按行优先顺序存储的线性序列为:

c语言是按行优先顺序存储的。
2.列优先顺序(Column Major Order):将数组元素按列向量排列,第j+1个列向量紧接在第j个列向量之后,对二维数组,按列优先顺序存储的线性序列位:

设有二维数组A=(aij)mxn ,若每个元素占用的存储单元数为 /(个),LOC[a11]表示元素a11的首地址(也可以用a00表示首地址),即数组的首地址。
1.以“行优先顺序”存储
(1)第1行中的每个元素对应的(首)地址是:
![]()
注:如果下标从0开始:LOC[a1j] = LOC[a11]+j x /
(2)第2行中的每个元素对应的(首)地址是:
![]()
注:如果下标从0开始:LOC[a2j] = LOC[a11]+(1xn)x/ + jx/
(3)第m行中的每个元素对应的(首)地址是:

注:如果下标从0开始:LOC[amj] = LOC[a11]+(mxn)x/ + jx/
三维数组中任一元素aijk的(首)地址是:
![]()
多维数组推而广之。
2.以“列优先顺序”存储
(1)第1列中的每个元素对应的(首)地址是:
![]()
(2)第2列中的每个元素对应的(首)地址是:

(3)第n列中的每个元素对应的(首)地址是:

特殊矩阵的压缩存储
特殊矩阵:是指非零元素或零元素的分布有一定规律的矩阵
对于高阶矩阵,若其中非零元素呈现某种规律分布或者矩阵中有大量的零元素,若仍然用常规方法存储,可能存储重复的非零元素或零元素,将造成存储空间的大量浪费。对这类矩阵进行压缩存储。
1.多个相同得非零元素只分配一个存储空间
2.零元素不分配空间
比如:一个nxn的二阶矩阵压缩成一个n的一维空间,大大减少了存储空间,即压缩存储。
1.对称矩阵
若一个n阶方阵A=(aij)nxn中的元素满足aij=aji ,i>=1,j<=n 且i≠j,则称A为对称矩阵
即:关于对角线对称

对称矩阵中的元素关于主对角线对称,因此,让每一对对称元素aij 和 aji(i≠j)分配一个存储空间,则n^2个元素压缩存储到
n(n+1) /2 个存储空间(即只存储下三角的元素,包含对角线即1+2+3+...+n=n(n+1) /2),能节约近一半的存储空间。
假设按“行优先顺序”存储下三角形(包括对角线)元素;设用一维数组(向量)sa[0....n(n+1)/2]存储n阶对称矩阵。为了便于访问,必须找出矩阵A中的元素下标值(i,j)和向量sa[k]的下标值k之间的对应关系。

若i>=j:aij 在下三角形中,直接保存在sa中。aij之前的i-1行共有元素个数:1+2+....+(i-1) = i(i-1)/2,在第i行上,aij之前恰有j-1个元素,因此,元素aij保存在向量sa中时的下标值k之间的对应关系是:
k=i x (i-1) /2 + j-1 (i>=j)
若i<j: 则aij是在上三角矩阵中。因为aij=aji,在向量sa中保存的是aji,即:
k=j x (j-1) /2 + i-1 (i<j)
所以,对称矩阵元素aij保存在向量sa中时的下标值k与(i,j)之间的对应关系是:

注意:此处i,j的下标均是从1开始的
如果下标从0开始则关系式:
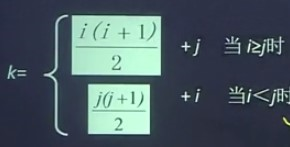
2.三角矩阵
(1)以主对角线划分,三角矩阵有上三角和下三角两种。
(2)上三角矩阵的下三角(不包括主对角线)中的元素均为常数c(一般为0),下三角矩阵正好相反,它的主对角线上方均为常数。

三角矩阵中的重复元素c可共享一个存储空间,其余元素正好有n(n+1) /2个,因此三角矩阵可压缩存储到向量sa[0...n(n+1) /2]中(一位数组),其中c存放在向量的最后1个分量重。
上三角矩阵元素aij保存在向量sa中时的下标k与(i,j)之间的对应关系是:
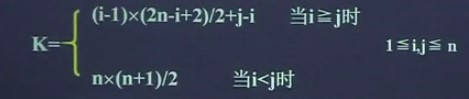
下三角矩阵元素aij保存在向量sa中时的下标值k与(i,j)之间的对应关系是:
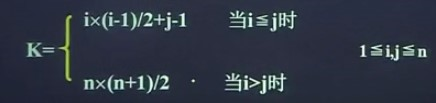
3.对角矩阵
矩阵中,除了主对角线和主对角线上或下方若干条对角线上的元素以外,其余元素皆为零。即所有的非零元素集中在以对角线为中心的带状区域中。

特点:以对角线为中心,第一行和最后一行都只有2个元素,其余每行都有三个元素,所以一个n行的对角矩阵中总数=3(n-2)+4 = 3n-2
对角矩阵可按行优先顺序或对角线顺序,将其压缩存储到一个向量中,并且也能找到每个非零元素和向量下标的对应关系,仍然以三对角矩阵为例讨论:当i=1,j=1、2, 当i=n,j=n-1、n,当1<i<n-1,j=i-1、i、i+1,其余元素都为0;
对这种矩阵,当以按“行优先顺序”存储时,第1行和第n行是2个非零元素,其余每行的非零元素都是3个,则需存储的元素个数为3n-2个。
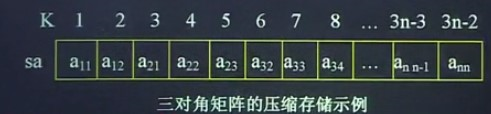
数组sa(sa从1开始)中的元素sa[k]与三对角矩阵中的元素aij (i,j从1开始)存在一一对应关系,在aij之前有i-1行,共有3x(i-1)-1个非零元素,在第i行,有j-i+1个非零元素(因为j-1=-1、0、1,所以j-i+1=0、1、2,即按这种位置顺序存储即可),这样,非零元素aij的地址位:
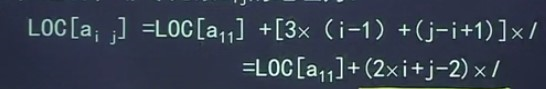
上例中,a34对应着sa[8],k=2xi+j-2=2x3+4-2=8
称sa[0....3n-2]是n阶三对角矩阵A的压缩存储。
稀疏矩阵
稀疏矩阵(Sparse Matrix):设矩阵A是一个nxm的矩阵中有s个非零元素,设 δ = s /(nxm),称矩阵δ为稀疏因子,如果某一矩阵的稀疏因子δ满足δ<=0.05时称为稀疏矩阵。

稀疏矩阵的压缩存储
对于稀疏矩阵,采用压缩存储方法时,只存储非0元素。须存储非0元素的行下标值、列下标值、元素值。
一个三元组(i,j,aij)唯一确定稀疏矩阵的一个非零元素。
1.三元组顺序表
若以行序为主序,稀疏矩阵中所有非0元素的三元组,就可以构成该稀疏矩阵的一个三元组顺序表。
相应的数据结构定义如下:
(1)三元组结点定义
元素节点

(2)三元组顺序表定义
信息总览结构

2.十字链表
对于稀疏矩阵,当非0元素的个数和位置在操作过程中变化较大时,采用链式存储结构表示比三元组的线性表更方便,矩阵中非0元素的结点所含的域有:行、列、值、行指针(指向同一行的下一个非0元)、列指针(指向同一列的下一个非0元)。其次,十字交叉链表还有一个头节点,结点结构如图所示。


结构定义

由定义知,稀疏矩阵中同一行的非0元素由right指针域链接成一个行链表,由down指针域链接成一个列链表。则每个非0元素既是某个行链表中的一个结点,同时又是某个列链表中的一个结点,所有非0元素构成一个十字交叉的链表。称为十字链表。
此外,还可用两个一维数组分别存储行链表的头指针和列链表的头指针。
优势:查找方便,缺点:复杂
广义表
广义表是线性表的推广和扩充,在人工智能领域中应用十分广泛。把线性表定义为n(n>=0)个元素a1,a2,....an的又穷序列,该序列中的所有元素具有相同得数据类型且只能是原子项。
所谓原子项可以是一个数或一个结构,是指结构上不可再分的。若放松对元素的这种限制,或许它们有其自身结构,就产生了广义表的概念。
广义表(Lists,又称为列表):是由n(n>=0)个元素组成的有穷序列:LS=(a1,a2,....an);其中ai 或者是原子项,或者是一个广义表。LS是广义表的名字,n为它的长度。若ai 是广义表,则称为LS的子表。习惯上:原子用小写字母,子表用大写字母。
定义非空广义表LS:
(1).a1(表中第一个元素)称为表头;
(2).其余元素组成的子表称为表尾;(a2,a3,a4....an)
(3).广义表中所包含的元素(包括原子和子表)的个数称为表的长度
(4).广义表中括号的最大层数称为表深(度)
(5).两个基本操作GetHead() :取表头元素;GetTail():取表尾
