积性函数:
一、定义
积性函数指对于所有互质的整数a和b有性质f(ab)=f(a)f(b)的数论函数。
二、常见的积性函数
φ(n) -欧拉函数,计算与n互质的正整数之数目
μ(n) -莫比乌斯函数,关于非平方数的质因子数目
gcd(n,k)-最大公因子,当k固定的情况
d(n) -n的正因子数目
σ(n) -n的所有正因子之和
σk(n)-因子函数,n的所有正因子的k次幂之和,当中k可为任何复数。
1(n) -不变的函数,定义为 1(n) = 1 (完全积性)
Id(n)-单位函数,定义为 Id(n) = n(完全积性)
Idk(n)-幂函数,对于任何复数、实数k,定义为Idk(n) = n^k(完全积性)
ε(n) -定义为:若n = 1,ε(n)=1;若 n > 1,ε(n)=0。别称为“对于狄利克雷卷积的乘法单位”(完全积性)
λ(n) -刘维尔函数,关于能整除n的质因子的数目
γ(n),定义为γ(n)=(-1)^ω(n),在此加性函数ω(n)是不同能整除n的质数的数目
性质:
1.若将n表示成质因子分解式
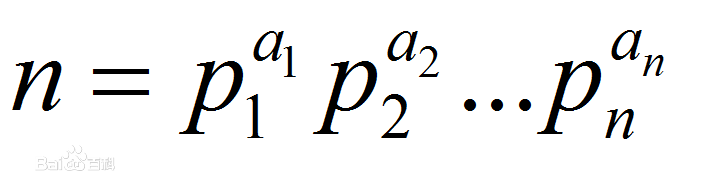
则有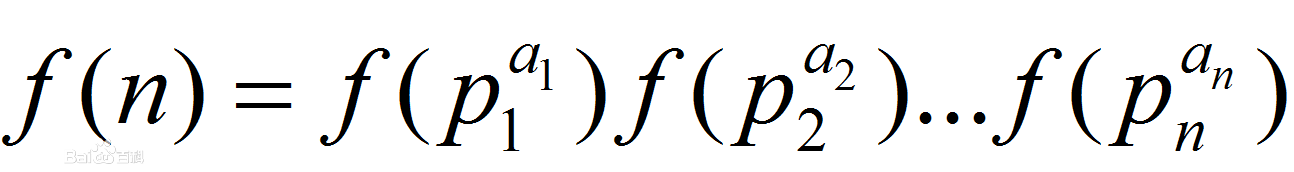
基本上都是通过这个性质做题,和欧拉筛差不多:
例1:传送门

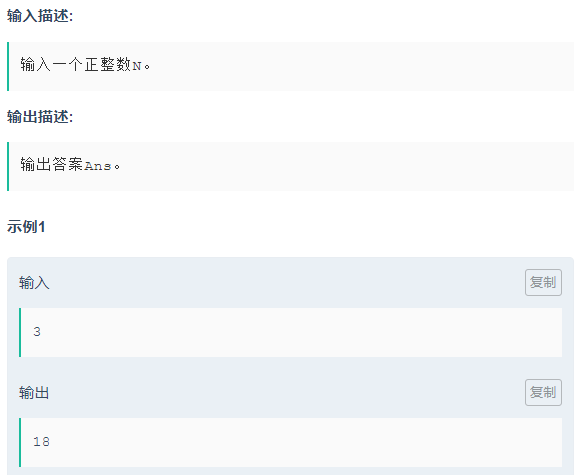
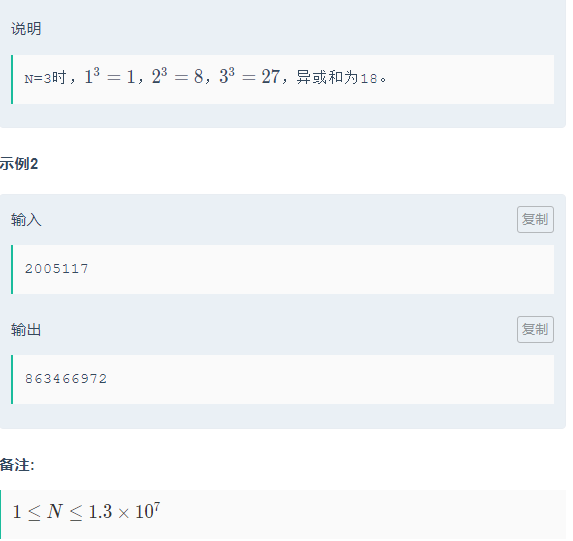
这是一个积性函数,满足f(a,b)=f(a)*f(b);
也就是说我们只要把所有质数的N次方算出来即可
合数可以通过质数得出
其他常见的积性函数还有
1.莫比乌斯函数
2.欧拉函数
3.求约数和
4.求约数的个数
#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=13000005; const int mod=1e9+7; ll prime[maxn],n,f[maxn]; bool biaoji[maxn]; int cnt; ll qpow(ll a,ll b){ ll ans=1; a%=mod; while(b){ if(b&1){ ans=(ans*a)%mod; } a=(a*a)%mod; b>>=1; } return ans; } void inint(ll n){ f[1]=1; for(int i=2;i<=n;i++){ if(!biaoji[i]){ prime[++cnt]=i; f[i]=qpow(i,n)%mod; } for(int j=1;j<=cnt&&i*prime[j]<=n;j++){ f[i*prime[j]]=(1ll*f[i]*f[prime[j]])%mod; biaoji[i*prime[j]]=true; if(i%prime[j]==0){ break; } } } } int main(){ scanf("%lld",&n); inint(n); ll ans1=0; for(int i=1;i<=n;i++){ ans1=ans1^f[i]; } printf("%lld ",ans1); }
链接:https://ac.nowcoder.com/acm/contest/392/C
来源:牛客网
输入描述:
输入一个正整数N。
输出描述:
输出答案Ans。
备注:
1≤N≤1.3×1071le Nle 1.3 imes10^71≤N≤1.3×107