和整数二分不同,浮点数不存在由于(整数)取整导致的边界问题,每次二分区间严格减半,
因此比整数二分简单的多,每次更新边界时直接让r = mid或l = mid即可。
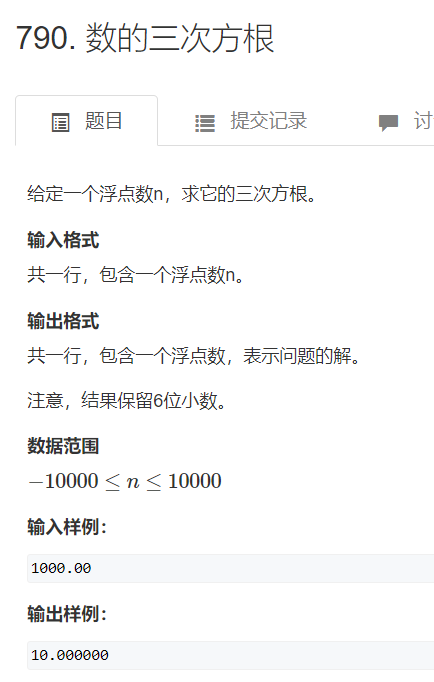
看一道题,acwing790.数的三次方根
浮点数二分除了更新区间和浮点数不同,还有就是二分终止条件,一般有两种写法,一种就是当前区间长度已经足够小。
比如这题需要保留六位小数,我们可以在区间长度小于1e-8时结束循环,一般区间长度比保留位数还要小两个数量级。
#include<iostream>
using namespace std;
int main() {
double x;
scanf("%lf", &x);
double l = -100, r = 100; //这题最大值和最小值分别是正负一百
while(r - l > 1e-8) {
double mid = (l + r) / 2;
if(mid * mid * mid >= x) {
r = mid; //可以发现浮点数二分更新区间比整数二分简单的多
} else {
l = mid;
}
}
printf("%.6lf
", l);
return 0;
}
还有一种写法,就是直接把二分迭代100次,也就是把while(r - l > 1e-8)换成for(int i = 0; i < 100; ++i)
这句话的意思是把区间缩小2100倍,由于2100是个很大的数,所以这样也能让区间变得很小。
#include<iostream>
using namespace std;
int main() {
double x;
scanf("%lf", &x);
double l = -100, r = 100;
for(int i = 0; i < 100; ++i) { //这是另一种浮点数二分的写法,直接对二分迭代多次,把区间缩小的足够小即可
double mid = (l + r) / 2;
if(mid * mid * mid >= x) {
r = mid;
} else {
l = mid;
}
}
printf("%.6lf
", l);
return 0;
}