不了解线段树的朋友可以看看我上一篇博客: [线段树系列] 普通线段树
补充一个上一篇漏了的点:线段树要开4倍空间。
然而面对庞大的数据我们开maxn<<2的空间是肯定开不下的。
这时候就要用到动态开点线段树来节省空间了。( 或者离散化 )
动态开点线段树大概长这样( 又是随手画的一个图 ):
理解一下就好,你写出来的也不长这样
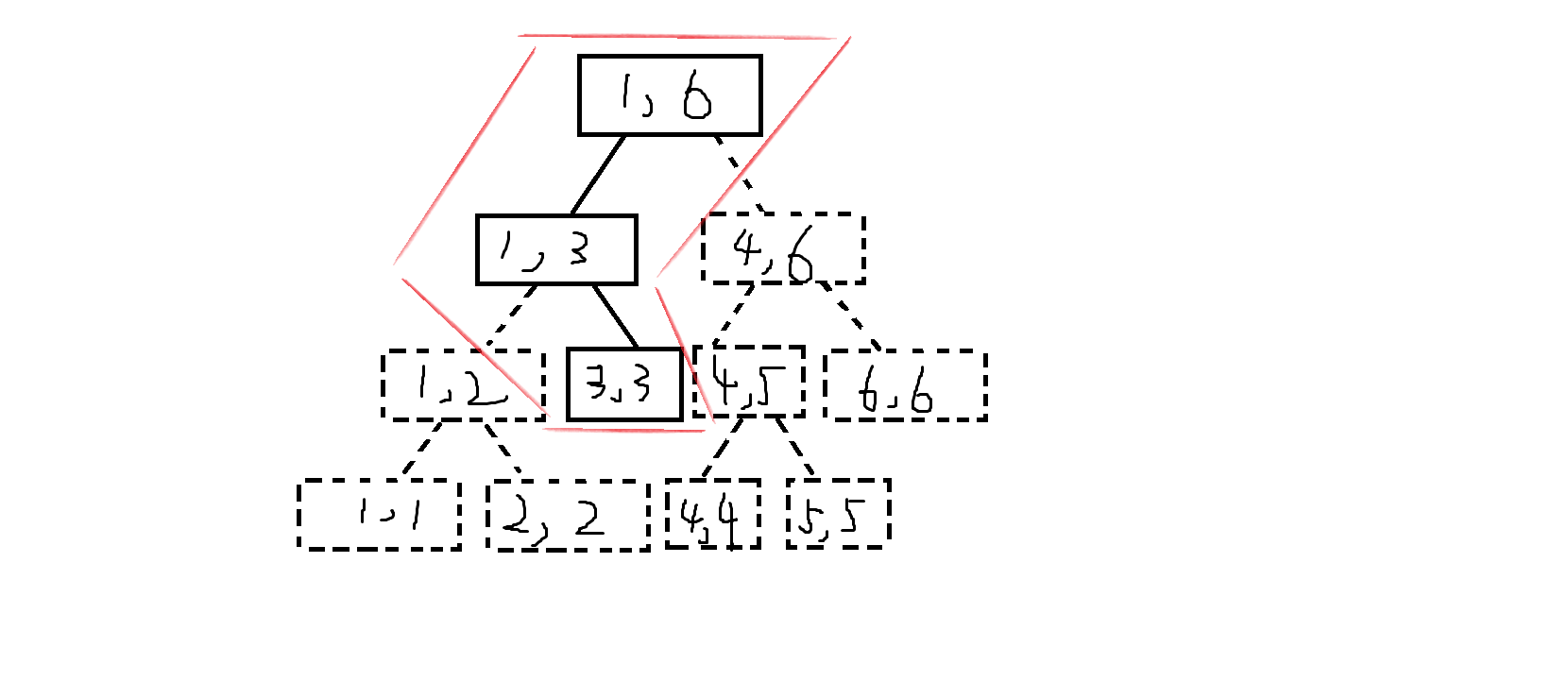
图中红色水彩线圈出来的就是你的动态开点线段树在某时间大概长的样子。
简单来说就是,你要用到一个点才开那个点,不用的点不开,可以大幅节省空间。
这样空间复杂度可以大致降到O(nlogn)。
是不是很棒。
接下来是实现:
一开始,你只有一个根节点。
通过update函数往树里面插点,开两个数组记录每个节点的左右儿子编号。
递归进入左右儿子,如果要用新点,就开新点。
上代码(以区间和为例):
插入
inline void update(int &o,int l,int r,int x,int val){
if(!o)o=++ncnt;
if(l==r){
sum[o]+=val;return;
}
int mid=(l+r)>>1;
if(x<=mid)update(lc[o],l,mid,x,val);
else update(rc[o],mid+1,r,x,val);
pushup(o);
}
查询
int ask(int o,int l,int r,int L,int R){
if(!o)return 0;
if(L<=l && R>=r)return sum[o];
int val=0;
int mid=(l+r)>>1;
if(L<=mid)val+=ask(lc[o],l,mid,L,R);
if(R>mid)val+=ask(rc[o],mid+1,r,L,R);
return val;
}
其它操作跟线段树是一样的,你只要把普通线段树里的p<<1换成lc[p],p<<1|1换成rc[p]就行了。
我上一篇的线段树也是记录了左右儿子编号的,其实没有必要,只是为了这一篇做个铺垫。
灵活运用动态开点线段树可以节省很多内存,而且能做到普通线段树做不到的事情。
比如题目要求在线操作不能离散化,值域又特别大:inf,并且询问q不大
这时候我们就可以用动态开点线段树开qloginf个点过掉这题。
是不是很美妙。
上代码:
#include<bits/stdc++.h>
#define LOG 20
using namespace std;const int maxn=100010;
int rt,ncnt,lc[maxn*LOG],rc[maxn*LOG],sum[maxn*LOG];
inline void pushup(int o){
sum[o]=sum[lc[o]]+sum[rc[o]];//更新
}
inline void update(int &o,int l,int r,int x,int val){
if(!o)o=++ncnt;//开点
if(l==r){
sum[o]+=val;return;
}
int mid=(l+r)>>1;
if(x<=mid)update(lc[o],l,mid,x,val);
else update(rc[o],mid+1,r,x,val);
pushup(o);
}
int ask(int o,int l,int r,int L,int R){
if(!o)return 0;//没这个点,直接返回0
if(L<=l && R>=r)return sum[o];
int val=0;
int mid=(l+r)>>1;
if(L<=mid)val+=ask(lc[o],l,mid,L,R);
if(R>mid)val+=ask(rc[o],mid+1,r,L,R);//递归计算
return val;
}
int main(){
int n;cin>>n;
for(int i=1;i<=n;i++){
int num;cin>>num;
update(rt,1,n,i,num);
}
int q;cin>>q;
while(q--){
int l,r;cin>>l>>r;
cout<<ask(rt,1,n,l,r)<<endl;
}
}
这个东西不难,我就不多说了,下一篇更新可持久化线段树( 主席树 )。
撰文不易,希望能帮到各位。本系列持续更新,求顶