神经元
3B1B先讨论最简单的MLP(多层感知器),只是经典的原版,就已经能识别手写数字。

这里一开始我们把神经元看作装有数字的容器,装着一个0~1之间的数字。但是最后更准确一些,我们把神经元看作一个函数,它输入的是上一层所有神经元的输出。
手写数字识别示例
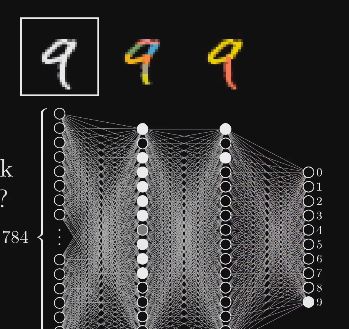
看下面这个手写数字的例子

这个神经网络一开始的地方有很多神经元,分别对应了$28 x 28$的输入图像中的每个像素,总共784个神经元。
神经元中装的数字代表对应像素的灰度值(0代表纯黑像素,1代表纯白像素),我们把神经元里装着的数叫做激活值(Activation)。这个784个神经元就组成了网络的第一层。
网络的最后一层的10个神经元分别代表0~9这10个数字,它们的激活值也同样介于0~1。这些值表示系统认为输入图像对应哪个数字的可能性。

网络中间还有几层隐含层,暂时看作暗箱。在这个网络中,3B1B加入两层隐含层,每层16个神经元。
神经网络运作的时候,上一层激活值决定下一层激活值。
为什么要分层
(视频在层数这里貌似不太严谨,输入层应该算作第0层)

先来看隐含层第二层
我们希望倒数第二层中的各个神经元分别对应上一个笔画部件。


再来看隐含层第一层
识别圆圈的任务同理可以拆分成更细微的问题。

于是我们希望网络第二层的各个神经元对应这些短边
但神经网络真的是这么做的吗?视频里提了这个问题,但貌似没有给出答案。
连线的作用
如何让第二层(隐含层的第一层)中的这一个神经元能够能够识别出图像的这一块区域是否存在一条边?

我们拿出第一层(输入层/第0层)的激活值,并赋上权重(要关注区域的权重为正值,否则为0),这样对所有像素值求加权和,就只会累加关注区域的像素值了。将这个加权和输入到$Sigmoid$函数。


情况一下子变得很糟,因为要考虑的东西很多

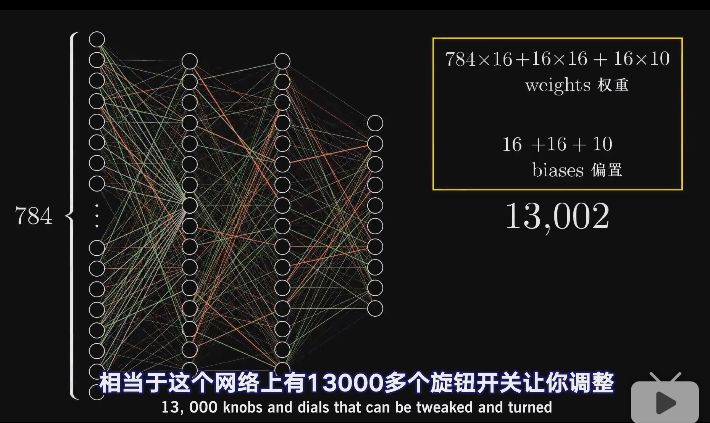
这里有13000多个参数需要调整,所以这里所谓的学习就是找到正确的权重和偏置。

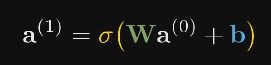
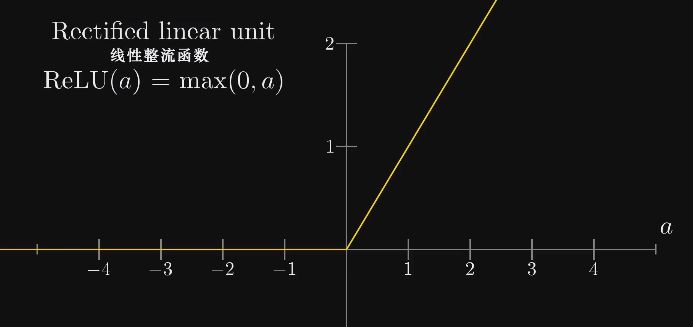
注:
现在的神经网络基本不用$sigmoid$函数了,用的是$ReLU$
参考链接: