神奇的树状数组

最近在学习位运算，正好把树状数组总结下，也算是能正式给data structure 建个分类。

那么，树状数组到底有什么用呢？诚然，一样没什么卵用的东西我们学它干嘛。

下面举个树状数组的经典应用：区间求和。

假设我们有如下数组（数组元素从 index=1 开始）:

 var a = [X, 1, 2, 3, 4, 5, 6, 7, 8, 9];

我们设定两种操作，modify(index, x) 表示将 a[index] 元素加上x， query(n, m) 表示求解 a[n] ~ a[m] 之间元素的和。如果不了解树状数组（当然假设更不了解线段树等其他数据结构），你可能会很容易地写下如下代码：

var a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];

function query(n, m) {
  var sum = 0;
  for (var i = n; i <= m; i++)
    sum += a[i];
  return sum;
}

function modify(index, x) {
  a[index] += x;
}

Ok，复杂度为O(1)的删改和复杂度为O(n)的查询。如果数据量很大，这样反复的查询是相当耗时的。我们退一步想，如果只有 query(n, m) 这个操作，很容易想到用sum数组预处理前n项的和，然后用 sum[m] - sum[n-1] 获得答案。但是如果要修改 a[index] 的值，因为该项影响所有index之后的sum数组元素，所以如果这样做复杂度变为O(1)的查询和O(n)的删改，并没有什么卵用。

但是这个思路是美好的，我们可以用一个sum数组保存一段特定的区间段的值。假设我们有 a[1] ~ a[9] 9个元素，我们根据一个特定的规则：

sum[1] = a[1];
sum[2] = a[1] + a[2];
sum[3] = a[3];
sum[4] = a[1] + a[2] + a[3] + a[4];
sum[5] = a[5];
sum[6] = a[5] + a[6];
sum[7] = a[7];
sum[8] = a[1] + a[2] + a[3] + a[4] + a[5] + a[6] + a[7] + a[8];
sum[9] = a[9];

如果要求 a[1] ~ a[9] 的和，即为 sum[9] + sum[8]，如果要求 a[1] ~ a[7] 的和，即为 sum[7] + sum[6] + sum[4] ，如果要改变 a[1] 的值，改变sum数组中和 a[1] 有关的项即可（即 sum[1] sum[2] sum[4] sum[8]）。 这就是树状数组！实现了O(logn)的查询和删改。但是如何将a数组和sum数组联系起来？

---

来观察这个图：

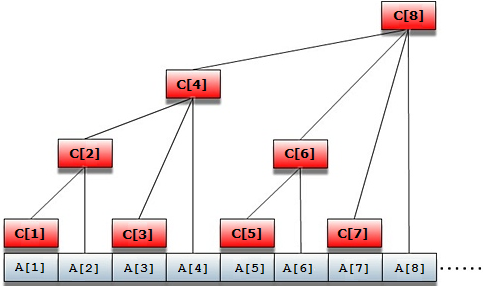
令这棵树的结点编号为C1，C2...Cn。令每个结点的值为这棵树的值的总和，那么容易发现（如上所说）：

C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8

这里有一个有趣的性质：设节点编号为x，那么这个节点管辖的区间为 2^k（其中k为x二进制末尾0的个数）个元素。因为这个区间最后一个元素必然为Ax，所以很明显：Cn = A(n – 2^k + 1) + ... + An，算这个2^{k有一个快捷的办法，定义一个函数如下即可（求解2}k即求二进制码右边第一位1的值）：

int lowbit(int x) {
  return x & (-x);
}

当想要查询一个SUM(n)(求a[1]~a[n]的和），可以依据如下算法即可：

1. 令sum = 0，转第二步；
2. 假如n <= 0，算法结束，返回sum值，否则sum = sum + Cn，转第三步；
3. 令n = n – lowbit(n)，转第二步。

可以看出，这个算法就是将这一个个区间的和全部加起来。

那么修改呢，修改一个节点，必须修改其所有祖先，最坏情况下为修改第一个元素，最多有log(n)的祖先。所以修改算法如下（给某个结点i加上x）：

1. 当i > n时，算法结束，否则转第二步；
2. Ci = Ci + x， i = i + lowbit(i)转第一步。i = i + lowbit(i)这个过程实际上也只是一个把末尾1补为0的过程。 对于数组求和来说树状数组简直太快了!

关于这部分的代码，将在下文树状数组的具体三大应用中给出。

关于树状数组，有一点需要注意，为了方便，树状数组的a数组基本都是从 index=1 开始的。

---

下文中楼主会分析下树状数组的三大应用场景：改点求段，改段求点，改段求段。