在渲染头发、丝绸等材质时,常要用到各向异性高光(Anisotropic highlighting)。什么是各向异性高光呢?先来个直观的对比,如下面图1、图2。
图1 普通的Blinn-Phong高光
图2 各项异性高光
图1和图2是在同一个场景里、同一个模型(一个球)、相机、光源(只有一个平行光),甚至它们的漫反射光照也一样,只有高光的计算方法不同。
图1使用的传统的Blinn-Phong高光,可以看到高光呈一个圆形亮光斑,比较集中。
// Blinn-Phong specular highlight
vec3 col = vec3(0.);
vec3 halfDir = normalize(viewDir + lightDir);
float nh = dot(normal, halfDir);
float spec = pow(nh, 100.);
col += nl * lightColor * albedo + specColor * spec;
图2中渲染的是各向异性高光,呈环形,在头发渲染中又称为“天使环”,这里使用的光照模型是Kajiya-Kay Model。在很多游戏中,头发渲染都使用了Kajiya-Kay Model,比如崩坏3(当然崩坏3在这个基础的模型基础上进行了一些创新,主要是一些参数的控制,我后面会说)。
// anisotropic highlighting
// http://web.engr.oregonstate.edu/~mjb/cs519/Projects/Papers/HairRendering.pdf
// 计算球在当前点的切线
vec3 tangent = SphereTangent(pos, normal);
// 切线偏移,可以移动“天使环”的位置,在上面链接里的PDF中详细说明,我不细说了
//float shift = texelFetch(iChannel0, ivec2(0), 0).r;
//shift = shift * 2. - 1.;
//tangent = ShiftTangent(tangent, normal, shift);
vec3 col = vec3(0.);
vec3 halfDir = normalize(viewDir + lightDir);
float dotTH = dot(tangent, halfDir);
// 关于dirAtten的计算说明见下文
float dirAtten = smoothstep(-1., 0., dotTH);
float sinTH = sqrt(1. - dotTH * dotTH);
// Kajiya-Kay Model
col += nl * lightColor * albedo + nl * dirAtten * specColor * pow(sinTH, 100.);
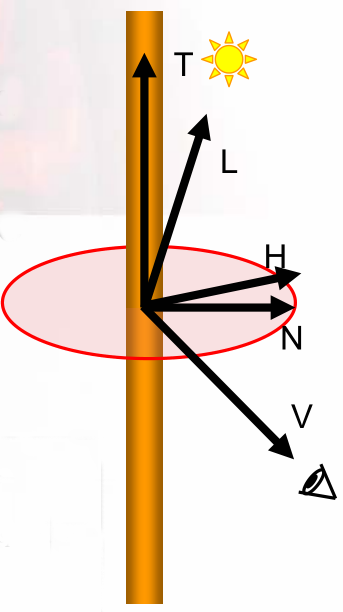
图3 Kajyiya-Kay Model
从上面代码来看Kajiya-Kay Model模型使用切线T和半角向量H(即代码中的halfDir)之间夹角的正弦值来计算高光系数(即pow(sinTH,100)),而不是Blinn-Phong中的法线和H向量之间夹角的余弦(即pow(nh, 100.))。
图3中,黄色的粗圆柱表示一根头发,T是其切线,V是视线,L是光源方向, H是L和V之间夹角的一半。其实T和H夹角的正弦恰好就是图3中H和N之间的余弦值,这样说来Kajiya-Kay Model本质上还是使用的余弦值来计算高光系数。但是值得注意的是在每根头发的固定点处,T总是保持不变的,N是随视线V变化而变化的,N总是在T和V组成平面内。也就是在一个被渲染的点处,其法线在各个(视线)方向是不同的,这大概所谓就是的“各向异性”。而我们之所以要有T就是为了计算出这个隐藏在背后的法线N。当然,我们不需要计算出这个N的确切值,其蕴含在T和H的正弦值中,V蕴含在H中。所以,我认为Kajiyaa-Kay Model本质上仍然是Blinn-Phong,只是它用切线T帮我们找到当前视线下的使高光最强的法线N。
另外,注意上面的方向衰减系数dirAtten的计算:
float dirAtten = smoothstep(-1., 0., dotTH);
为什么要这么计算?貌似好多人都只知道这是个衰减系数,而不知道为什么要这样计算,或者说不太清楚背后的几何意义。这个方向衰减系数其实涉及到两个方向,一个是光源的方向L,一个是视线方向V,它们都蕴含在H中。首先,这里smoothstep的第3个参数传的是dotTH,即切线和和H的余弦值。而这里smoothstep的第1个参数-1表明当dotTH小于或等于-1时(实际上最多等于-1,不会比-1还小,因为所有参与计算的向量都是规范化的),dirAtten值为0。什么时候dotTH为-1呢,就是图3中,H的方向恰好和T的方向相反时,这时候T和H之间的夹角为180度。而smoothstep的第2个参数0表明当dotTH大于或等于0时,dirAtten的值为1。注意dotTH最大值为1,此时T和H的方向刚好相同,两者之间的夹角为0度。所以smoothstep(-1., 0., dotTH)的作用就是取和切线T角夹在0至180度之间的H。当T和H之间的夹角不在这个范围内时,必然出现H和对应N的点积小于0,即此时高光为0 (此时光源照不到当前着色点或相机看不到当前着色点),此时dirAtten的值就应当为0(即没有高光)。
另外,一般的我们可以定制各向异性高光的参数,比如计算各向异性高光时dirAtten * specColor * pow(sinTH, 100.);,其中的100就是一个可调参数,这个参数值越大,“天使环”的越细,其值越大,“天使环”越宽。这一点大家都可以理解。而我们可以更进一步,直接使用一张贴图来控制“天使环”在各处的宽度,使其在各处的宽度不同,甚至可以把“天使环”调成各种有趣的图案,以达到想要的艺术效果。还有渲染头发一般有两个“天”使环,第二个会较暗一些,且是有自己的颜色的,更靠近发根。只要理解了第一个“天使环”的原理,第二个只是在第一个基础上进行了偏移,颜色稍微有点不同而已,我不再赘述。
我写了一个Shadertoy: Anisotropic highlighting (shadertoy.com),有源代码,在电脑上打开浏览器,可在线运行,可进行交互,调整天使环的位置,希望能帮助到一些同学。如果因为某些原因,打不开网址,我也录制了一个[视频](A shdertoy: Anisotropic Hightlighting - 知乎 (zhihu.com)),可在知乎上观看。
最后,我想记录一下在写这个Shadertoy时用到的一个小技巧: 球的切线的计算。
在代码中,那个红色的球是用数学公式建模的即 $ length(p - center) = r$,然后从相机处发射射线,判断射线与球是否相交以及距相机的距离,来求得交点,即当前着色点。法线的计算很简单,不赘述。但是怎么计算出切线呢?我是这样做的: 用当前着色点的三维坐标及其法线确定一个平面,然后把当前着色点的y坐标加1(当然加别的数值应该也可以)得到偏移后的一个点,然后把这个偏移后的点再投影到刚刚确定的那个平面上,则投影得到点减去当前着色点得到的向量就是当前着色点的一个切线向量,进行规范化即可。关于平面方程及点投影到平面,可参考这篇文章:平面(Plane) - 知乎 (zhihu.com)。
代码如下:
// pos是当前着色点的三维坐标
vec3 SphereTangent(vec3 pos, vec3 normal) {
vec3 posOffseted = pos;
posOffseted.y += 1.;
float D = - dot(normal, pos);
float distToPlane = dot(normal, posOffseted) + D;
vec3 proj = posOffseted - normal * distToPlane;
vec3 tangent = normalize(proj - pos);
return tangent;
}
我不知道有没有人这样做过,我是临时想到的,实现了一下效果还行。
参考:

