随着时代的进步与科技的发展,天气逐渐成为人们讨论的话题,而天气的预测在今天已经成为网络世界里最为人关注的问题之一。通过某地每日最高气温和每日最低气温的研究可实现预测天气、预测自然灾害等功能。如研究多地的气温关系,包括地方和地方之间的气温关系、每日最高气温和每日最低气温的关系可得出很多有用的结论。如简单研究则得不出较深的结论,如通过笔算等形式进行分析则效率较低,所以本文通过专业的统计分析软件来对气温进行分析。本文通过SPSS软件对南京市、苏州市、金华市的每日最高气温和每日最低气温进行典型相关分析,对软件生成的报告进行简单的分析从而得出结论。(典型相关分析的基本概念、SPSS软件)
为研究南京市、苏州市、金华市的每日最高气温和每日最低气温的关系,对这三地的2021年10月的每日最高气温和每日最低气温进行搜集,单位为摄氏度。南京市、苏州市、金华市的每日最高气温形成第一组变量;而南京市、苏州市、金华市的每日最低气温形成第二组变量。
首先从Excel表导入数据,导入后如下图所示。
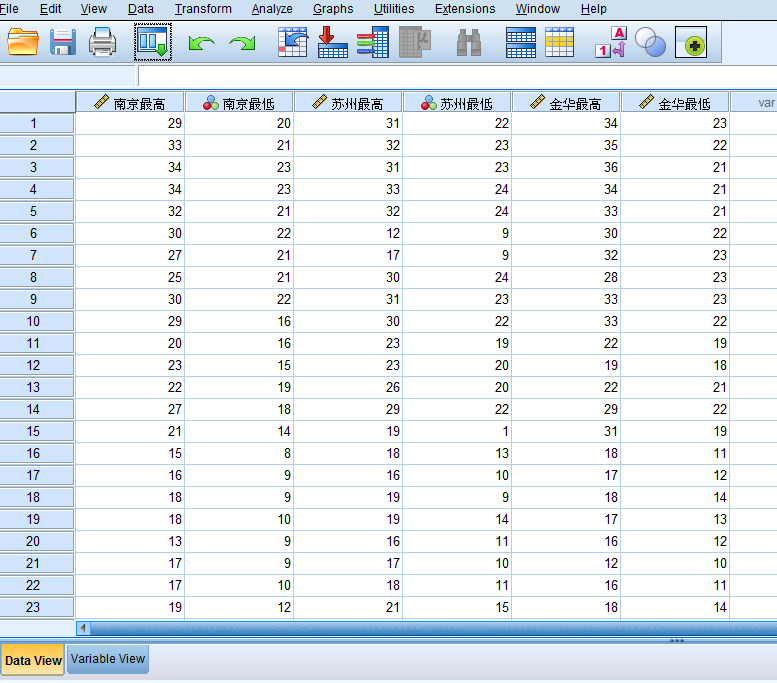
然后切换到变量视图,将Measure统一改为Scale。

然后依次选择Analyze-Correlate-Canonical Correlation。
在弹出的对话框中设置两组变量和其他设置,确定后可输出报告。
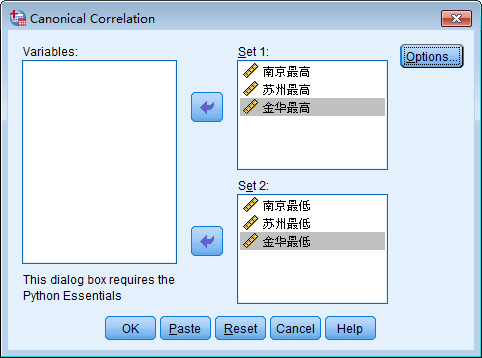
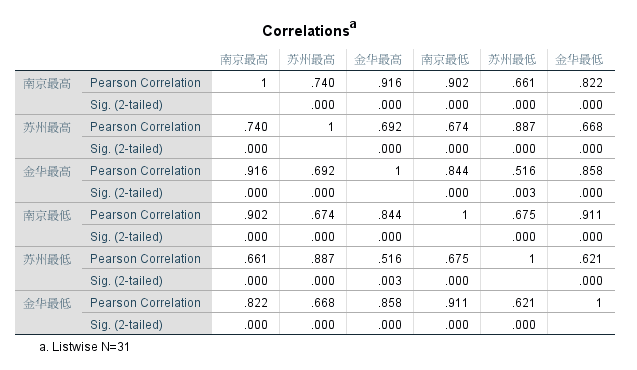
根据总表可以看出,每组变量内部和组与组之间的相关系数都较高。 根据典型相关系数表可以看出,前三个典型相关系数是显著的。 根据标准化相关系数可知,第一对典型变量u1和v1,标准化的表达式是u1=-0.779*南京最高-0.810*苏州最高+0.620*金华最高,v1=-0.311*南京最低-0.843*苏州最低+0.106*金华最低。 根据非标准化相关系数可知,第一对典型变量u1和v1,非标准化的表达式是u1=-0.132*南京最高-0.136*苏州最高+0.089*金华最高,v1=-0.059*南京最低-0.134*苏州最低+0.022*金华最低。 根据已解释的方差比例可知,统一看第一个典型变量,最高气温被自身解释了66.6%,被最低气温解释了57.2%。最低气温被自身解释了69.2%,被最高气温解释了59.4%。(部分报告图未展示)