Wolsey“强整数规划模型”经典案例之一单源固定费用网络流问题
阅读本文可以理解什么是“强”整数规划模型。
单源固定费用网络流问题见文献[1]第13.4.1节(p229-231),是"强整数规划建模“的极好案例。
本文是本博客原创,本博客不转贴他人作品。
单源固定费用网络流问题(The Signle Source Fixed Charge Network Flow Problem)
单源固定费用网络流问题:给定一个有向网络 (边数为m,节点数n),网络上只有一个流量流入节点(标记为1),但有若干个流量流出节点, 节点 i 的流出流量标记为 B[i], 每个边 e (e =1,...,m) 有流量限制(此例中不考虑流量限制,因此流量限制取为-B[1]) 。网络情况如下图:
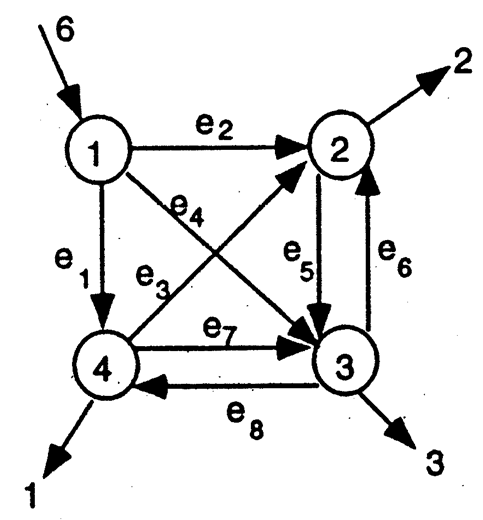
网络的节点数n=4, 边数m=8。
对应节点1,2,3,4, 流(出)量B={ -6 2 3 4}。
对应边e=1,2,3,4,5,6,7,8, 边由节点对定义,数据是 E={(1 4) (1 2) (4 2) (1 3) (2 3) (3 2) (4 3) (3 4)}.
对应边e=1,2,3,4,5,6,7,8, 边上的一次性费用是C={5 2 7 3 2 4 9 12}.
非“强”整数规划模型
设非负变量 x[e] 是边e (e =1,...,8) 上的流量, 又设0-1变量 y[e] 表示边e上是否有流量。于是模型的目标是极小化一次性费用和,约束无外乎节点上的流量平衡约束和x[e]-y[e]之间的关联约束。
用+Leapms写出模型,其PDF摘录如下:

上述模型用+Leapms中的solve命令求松弛解,可以看到y变量非0-1:
+Leapms>solve The LP is solved to optimal. 找到线性规划最优解.非零变量值和最优目标值如下: ......... x1*=1 x2*=2 x4*=3 y1*=0.166667 y2*=0.333333 y4*=0.5 ......... Objective*=3 ......... +Leapms>
若要获得整解则必须使用mip命令对问题进行分支定界/割平面求解:
+Leapms>mip relexed_solution=3; number_of_nodes_branched=0; memindex=(1,1) The Problem is solved to optimal as an MIP. 找到整数规划的最优解.非零变量值和最优目标值如下: ......... x1* =1 x2* =5 x5* =3 y1* =1 y2* =1 y5* =1 ......... Objective*=9 ......... +Leapms>
结果在网络上表现:
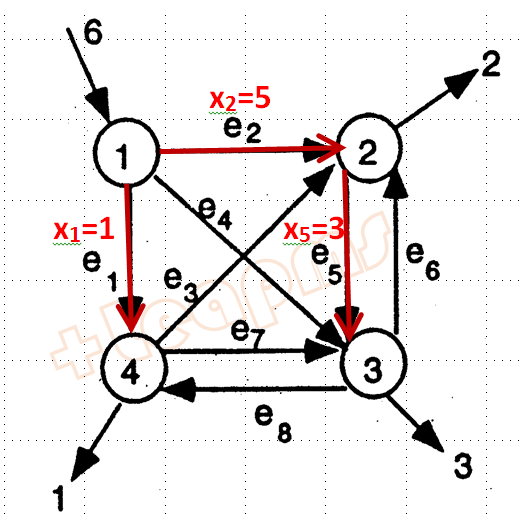
“强”整数规划模型(Strong Integer Formulation)
“强”整数规划模型对上述模型采用了Multicommodity改写。方法是引入一个新非负变量 z[e][k], 其含义是流过e边最终贡献给k节点流出的流量(显然此处k=2,...,n, k$ eq 1$)。
新模型的目标不会改变,约束中的节点平衡条件逻辑上也不改变,即对任何节点 i , 流出和流入之差应该为0 或者 当i==k时等于k的流出量。
用+Leapms写出模型,其PDF摘录如下:

上述所谓“强”模型比之前的模型的好处在于在+Leapms中直接使用solve命令就可以求出整数解,即不需要分支定界/割平面过程!
不十分严格地:此即是“强”整数规划模型和含义,强模型更容易求解,或者说对求解器更友好。
+Leapms的求解过程:
+Leapms>solve The LP is solved to optimal. 找到线性规划最优解.非零变量值和最优目标值如下: ......... x1*=1 x2*=5 x5*=3 y1*=1 y2*=1 y5*=1 z1_4*=1 z2_2*=2 z2_3*=3 z5_3*=3 ......... Objective*=9 ......... +Leapms>
结果在网络上表现:
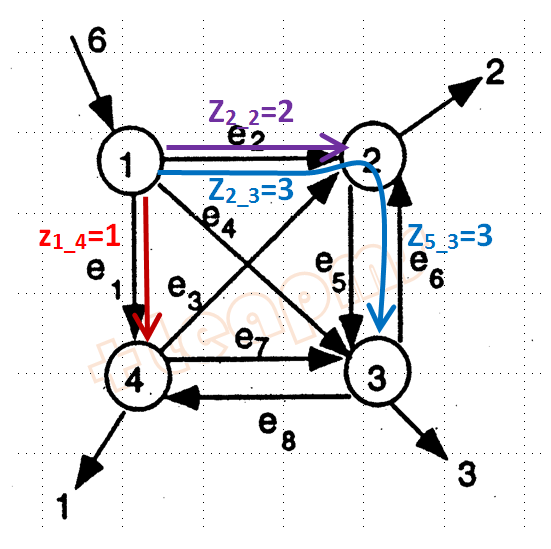
强整数规划模型的详细解释 及 “强”建模原理
本案例的“强”建模原理来源于文[1]中的三个观察(Oberservation 13.2-13.4, page 230) 。
关于“强”模型的详细解释,见文[2]。
其他
文[1]并未在13.4.1中给出此案例的所有数据,其余数据(主要是边上费用数据C是从13.1, page 222)的XPRESS MP模型中读出的。贴在这里,供看官与+Leapms建模语言作对比:


结论
“强”整数规划建模概念是经典建模方法中的重要内容,如果说在本科《运筹学》教学中只要讲述0-1变量的应用即可,那么在研究生层次的《高级运筹学》教学中最好增加“强”整数规划建模内容。
使用本土完全自主知识产权的+Leapms建模语言和+Leapms求解器,可以有效辅助教学,比之传统的舶来建模语言和求解器有优势。
参考文献
[1] Wolsey L A. Integer Programming. New York: Jonh Wiley & Sons, 1998 / ISBN 978-0-471-28366-9
[2] Wolsey L . Strong formulations for mixed integer programming: A survey[J]. Mathematical Programming, 1989, 45(1-3):173-191.