0 简介
本文介绍了HMM算法。
1 简单的理解
HMM 算法,名为「隐马尔科夫模型」。
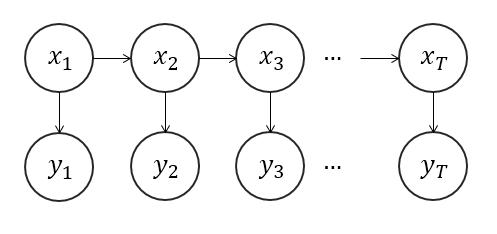
类似这张图片:
[Q={q_1,q_2,…,q_N},V={v_1,v_2,…,v_M}
]
[I=(i_1,i_2,…,i_T),O=(o_1,o_2,…,o_T)
]
名称的:
状态序列是隐藏的,图里使用 X 表示,所有的 x 都来自 Q.
观测序列是实际看到的,使用 Y 表示。所有的 y 都来自 V.
确定的:
(I)是长度为T的状态序列。
(O)是长度为T的观测序列。
状态转移的概率是:
[a_{ij}=P(i_{t+1}=q_j|i_t=q_i)
]
所有状态之间的转移概率,可以写成矩阵形式:
[A=[a_{ij}]_{N×N}
]
观测状态生成的概率是:
[b_j(k)=P(o_t=v_k|i_t=q_j)
]
每个隐状态,都可能生成不同的观测状态,写成矩阵形式为:
[ B=[b_j(k)]_{N×M}
]
另外,还有隐状态的初始概率:
[π_i=P(i_1=q_i)
]
感冒的例子
病人状态Q:感冒,非感冒。
病人感觉V:正常,头晕,冷。
入院检查:pi (初始状态)
概率如图:
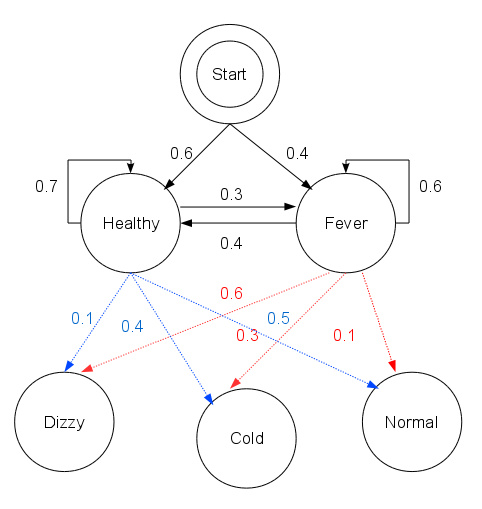
首先,定义状态,观测,以及转移等概率。
import numpy as np
# 状态集合Q
states = ('Healthy', 'Fever')
# 观测集合V
observations = ('normal', 'cold', 'dizzy')
# 初始状态概率向量π
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
# 状态转移矩阵A
transition_probability = {
'Healthy': {'Healthy': 0.7, 'Fever': 0.3},
'Fever': {'Healthy': 0.4, 'Fever': 0.6},
}
# 观测概率矩阵B
emission_probability = {
'Healthy': {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
'Fever': {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
}
由于,fever 等 label 是字符串,应该转化为纯数字 index 的形式。
# 这个步骤,将所有遇到的文字label,转化为index 数字的形式
def generate_idx_map(labels):
id2label = {}
label2id = {}
i = 0
# 遍历所有 labels
for l in labels:
id2label[i] = l
label2id[l] = i
i += 1
return id2label, label2id
# 使用这个函数
states_id2label, states_label2id = generate_idx_map(states)
observations_id2label, observations_label2id = generate_idx_map(observations)
# 打印结果
print(states_id2label, states_label2id)
print(observations_id2label, observations_label2id)
打印的结果是:
{0: 'Healthy', 1: 'Fever'} {'Healthy': 0, 'Fever': 1}
{0: 'normal', 1: 'cold', 2: 'dizzy'} {'normal': 0, 'cold': 1, 'dizzy': 2}
现在将定义好的转移,观测概率转化为矩阵形式:
def convert_map_to_vector(map_, label2id):
"""将概率向量从dict转换成一维array"""
v = np.zeros(len(map_), dtype=float)
for e in map_:
v[label2id[e]] = map_[e]
return v
def convert_map_to_matrix(map_, label2id1, label2id2):
"""将概率转移矩阵从dict转换成矩阵"""
m = np.zeros((len(label2id1), len(label2id2)), dtype=float)
for line in map_:
for col in map_[line]:
# 通过label转id函数,将字典中的概率,放置在相应的位置
m[label2id1[line]][label2id2[col]] = map_[line][col]
return m
# 生成矩阵
A = convert_map_to_matrix(transition_probability, states_label2id, states_label2id)
B = convert_map_to_matrix(emission_probability, states_label2id, observations_label2id)
observations_index = [observations_label2id[o] for o in observations]
pi = convert_map_to_vector(start_probability, states_label2id)
# 打印结果
print(B)
print(A)
print(pi)
[[ 0.7 0.3]
[ 0.4 0.6]]
[[ 0.5 0.4 0.1]
[ 0.1 0.3 0.6]]
[ 0.6 0.4]
随机生成观测序列和状态序列
# 输入是时间
def simulate(T):
def draw_from(probs):
# 按照多项式分布,生成数据
# multinomial 根据概率,给 sample
# where 输出满足条件的 value 位置
return np.where(np.random.multinomial(1,probs) == 1)[0][0]
# 根据T长度,定义obs和状态
observations = np.zeros(T, dtype=int)
states = np.zeros(T, dtype=int)
# 初始化状态
states[0] = draw_from(pi)
# 初始化输出
# 通过 B ,获得 states[0] 状态的发射or输出概率,并获得 obs 状态。
observations[0] = draw_from(B[states[0],:])
for t in range(1, T):
# 用上一个状态,在A中查找对应的转移概率
states[t] = draw_from(A[states[t-1],:])
# 输出 or 发射,同理
observations[t] = draw_from(B[states[t],:])
return observations, states
observations_data, states_data = simulate(10)
print(observations_data)
print(states_data)
生成并打印,相应的label
print("病人的状态: ", [states_id2label[index] for index in states_data])
print("病人的观测: ", [observations_id2label[index] for index in observations_data])
[0 0 1 1 2 1 2 2 2 0]
[0 0 0 0 1 1 1 1 1 0]
病人的状态: ['Healthy', 'Healthy', 'Healthy', 'Healthy', 'Fever', 'Fever', 'Fever', 'Fever', 'Fever', 'Healthy']
病人的观测: ['normal', 'normal', 'cold', 'cold', 'dizzy', 'cold', 'dizzy', 'dizzy', 'dizzy', 'normal']
HMM三个问题
-
概率计算问题:
已知模型 (λ=(A,B,π)) 和特定的观测序列 (O=o_1,o_2,...,o_T),从而计算 (P(O|λ)). -
学习问题:
已知 特定的观测序列 (O=o_1,o_2,...,o_T), 估算 (λ=(A,B,π)),从而让 (P(O|λ)) 最大。(在计算P(O|λ)时,其实就是解决 概率计算问题) -
预测问题(解码问题):
已知模型 (λ=(A,B,π)) 和特定的观测序列 (O=o_1,o_2,...,o_T),找到能够让(P(I|O))最大 的 状态序列I。