You have N integers, A₁, A₂, ... , A_N. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A₁, A₂, ... , A_N. -1000000000 ≤ A_i ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of A_a, A_a₊₁, ... , A_b. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of A_a, A_a₊₁, ... , A_b.

You need to answer all Q commands in order. One answer in a line.

The sums may exceed the range of 32-bit integers.

POJ Monthly--2007.11.25, Yang Yi

View Code

/*
 * POJ 3468 A Simple Problem with Integers
 * 经典的线段树题目，用splay tree来作为入门题
 * 成段更新+区间求和
 * 题目给定了n个数A1,A2,...An，有以下两种操作
 * C a b c:把c加入到Aa,Aa+1,..Ab中
 * Q a b:查询Aa,Aa+1,..Ab的和
 * 需要的变量：pre,ch,size(这三个基本都要),key(保存结点的值),sum(子树值和),add(增量的标记)
 * (一般标记类，正确的做法都是要先更新掉该点，标记是标记没有更新子结点)
 */

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define Key_value ch[ch[root][1]][0]
const int MAXN=100010;
int pre[MAXN],ch[MAXN][2],size[MAXN],root,tot1;//父结点、左右孩子、子树规模、根结点、结点数量
int key[MAXN];//该点的值
int add[MAXN];//增量的延迟标记
long long sum[MAXN];//子树的和
int s[MAXN],tot2;//内存池、内存池容量（这题用不到，如果有删除操作，内存不够可以这样

int a[MAXN];//初始的数组，建树时候用
int n,q;
//debug部分
void Treavel(int x)
{
    if(x)
    {
        Treavel(ch[x][0]);
        printf("结点%2d:左儿子 %2d 右儿子 %2d 父结点 %2d size=%2d,key=%2d add=%2d sum=%I64d\n",x,ch[x][0],ch[x][1],pre[x],size[x],key[x],add[x],sum[x]);
        Treavel(ch[x][1]);
    }
}
void debug()
{
    printf("root:%d\n",root);
    Treavel(root);
}
//以上是debug
void NewNode(int &r,int father,int k)//一个是调用的时候注意变量顺序，还有r必须引用&
{
    if(tot2)r=s[tot2--];//取得时候是tot2--,那么存的时候就要是++tot2
    else r=++tot1;
    pre[r]=father;
    size[r]=1;//这个不能忘记 ,一定是1，否则可能出错
    key[r]=k;
    add[r]=0;
    sum[r]=0;
    ch[r][0]=ch[r][1]=0;
}
//给r为根的子树增加值，一定把当前结点的全部更新掉，再加个延迟标记表示儿子结点没有更新
void Update_Add(int r,int ADD)
{
    if(r==0)return;
    add[r]+=ADD;
    key[r]+=ADD;
    sum[r]+=(long long)ADD*size[r];
}
//通过孩子结点更新父亲结点
void Push_Up(int r)
{
    size[r]=size[ch[r][0]]+size[ch[r][1]]+1;
    sum[r]=sum[ch[r][0]]+sum[ch[r][1]]+key[r];
}
//将延迟标记更新到孩子结点
void Push_Down(int r)
{
    if(add[r])
    {
        Update_Add(ch[r][0],add[r]);
        Update_Add(ch[r][1],add[r]);
        add[r]=0;
    }
}
//建树
//先建立中间结点，再两端的方法
void Build(int &x,int l,int r,int father)
{
    if(l>r)return;
    int mid=(l+r)/2;
    NewNode(x,father,a[mid]);
    Build(ch[x][0],l,mid-1,x);
    Build(ch[x][1],mid+1,r,x);
    Push_Up(x);
}
//初始化，前后各加一个king结点
void Init()
{
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    root=tot1=tot2=0;
    ch[root][0]=ch[root][1]=pre[root]=size[root]=add[root]=sum[root]=0;
    key[root]=0;
    NewNode(root,0,-1);
    NewNode(ch[root][1],root,-1);//头尾各加入一个空位
    Build(Key_value,1,n,ch[root][1]);
    Push_Up(ch[root][1]);
    Push_Up(root);
}
//旋转，0为左旋，1为右旋  该部分基本固定
void Rotate(int x,int kind)
{
    int y=pre[x];
    Push_Down(y);
    Push_Down(x);//先把y的标记向下传递，再把x的标记往下传递
    ch[y][!kind]=ch[x][kind];
    pre[ch[x][kind]]=y;
    if(pre[y])
        ch[pre[y]][ch[pre[y]][1]==y]=x;
    pre[x]=pre[y];
    ch[x][kind]=y;
    pre[y]=x;
    Push_Up(y);//维护y结点
}
//Splay调整，将结点r调整到goal下面
void Splay(int r,int goal)
{
    Push_Down(r);
    while(pre[r]!=goal)
    {
        if(pre[pre[r]]==goal)
            Rotate(r,ch[pre[r]][0]==r);
        else
        {
            int y=pre[r];
            int kind=ch[pre[y]][0]==y;
            if(ch[y][kind]==r)
            {
                Rotate(r,!kind);
                Rotate(r,kind);
            }
            else
            {
                Rotate(y,kind);
                Rotate(r,kind);
            }
        }
    }
    Push_Up(r);
    if(goal==0)root=r;
}
//得到第k个结点
int Get_Kth(int r,int k)
{
    Push_Down(r);
    int t=size[ch[r][0]]+1;
    if(t==k)return r;
    if(t>k)return Get_Kth(ch[r][0],k);
    else return Get_Kth(ch[r][1],k-t);
}
int Get_Min(int r)
{
    Push_Down(r);
    while(ch[r][0])
    {
        r=ch[r][0];
        Push_Down(r);
    }
    return r;
}
int Get_Max(int r)
{
    Push_Down(r);
    while(ch[r][1])
    {
        r=ch[r][1];
        Push_Down(r);
    }
    return r;
}
//区间增加一个值
//注意因为在前面增加了个结点，所以把第l个结点旋转到根结点，第r+2个结点旋转到根结点的右孩子，
//那么Key_value(ch[ch[root][1]][0]刚好就是区间[l,r]
void ADD(int l,int r,int D)
{
    Splay(Get_Kth(root,l),0);//第l个点到根结点
    Splay(Get_Kth(root,r+2),root);//第r+2个点到根结点的右孩子
    Update_Add(Key_value,D);
    Push_Up(ch[root][1]);
    Push_Up(root);
}
//查询区间的和
long long Query_Sum(int l,int r)
{
    Splay(Get_Kth(root,l),0);//第l个点到根结点
    Splay(Get_Kth(root,r+2),root);//第r+2个点到根结点的右孩子
    return sum[Key_value];
}

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    while(scanf("%d%d",&n,&q)==2)
    {
        Init();//这个不能忘记
        while(q--)
        {
            char op[20];
            int x,y,z;
            scanf("%s",op);
            if(op[0]=='Q')
            {
                scanf("%d%d",&x,&y);
                printf("%I64d\n",Query_Sum(x,y));
            }
            else
            {
                scanf("%d%d%d",&x,&y,&z);
                ADD(x,y,z);
            }
        }
    }
    return 0;
}

2、营业额统计（一个一个数插入，找出和这个数最接近的）

营业额统计

Description

营业额统计 Tiger最近被公司升任为营业部经理，他上任后接受公司交给的第一项任务便是统计并分析公司成立以来的营业情况。 Tiger拿出了公司的账本，账本上记录了公司成立以来每天的营业额。分析营业情况是一项相当复杂的工作。由于节假日，大减价或者是其他情况的时候，营业额会出现一定的波动，当然一定的波动是能够接受的，但是在某些时候营业额突变得很高或是很低，这就证明公司此时的经营状况出现了问题。经济管理学上定义了一种最小波动值来衡量这种情况：该天的最小波动值当最小波动值越大时，就说明营业情况越不稳定。而分析整个公司的从成立到现在营业情况是否稳定，只需要把每一天的最小波动值加起来就可以了。你的任务就是编写一个程序帮助Tiger来计算这一个值。第一天的最小波动值为第一天的营业额。 l 输入输出要求

Input

第一行为正整数，表示该公司从成立一直到现在的天数，接下来的n行每行有一个正整数，表示第i天公司的营业额。

Output

输出文件仅有一个正整数，即Sigma(每天最小的波动值) 。结果小于2^31 。

Sample Input

6

5

1

2

5

4

6

Sample Output

12

Hint

结果说明：5+|1-5|+|2-1|+|5-5|+|4-5|+|6-5|=5+4+1+0+1+1=12

这道题目很其他的比起来太简单了。。。

随便写、、

View Code

/*
 * 这题的意思就是每插入一个数，累加和前面插入的数的差值。第一个数加本身。
 * 用splay tree找寻前驱和后继。
 * 但是这题的splay tree按照key值得大小建立。
 * 我的做法是把这个数插入进去，找前驱和后继，其中一个就是最接近的了。
 * 这样做有了重复的元素，但是没有影响的
 * 这种题目用STL的set 、 SBT等都很好过了
 */
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int INF=0x3f3f3f3f;
const int MAXN=1000010;
int pre[MAXN],ch[MAXN][2],key[MAXN];
int root,tot1;

void NewNode(int &r,int father,int k)
{
    r=++tot1;
    pre[r]=father;
    ch[r][0]=ch[r][1]=0;
    key[r]=k;
}
void Init()
{
    root=tot1=0;
    ch[root][0]=ch[root][1]=key[root]=pre[root]=0;
}
//旋转
void Rotate(int x,int kind)
{
    int y=pre[x];
    ch[y][!kind]=ch[x][kind];
    pre[ch[x][kind]]=y;
    if(pre[y])
        ch[pre[y]][ch[pre[y]][1]==y]=x;
    pre[x]=pre[y];
    ch[x][kind]=y;
    pre[y]=x;
}
//Splay调整
void Splay(int r,int goal)
{
    while(pre[r]!=goal)
    {
        if(pre[pre[r]]==goal)
            Rotate(r,ch[pre[r]][0]==r);
        else
        {
            int y=pre[r];
            int kind=ch[pre[y]][0]==y;
            if(ch[y][kind]==r)
            {
                Rotate(r,!kind);
                Rotate(r,kind);
            }
            else
            {
                Rotate(y,kind);
                Rotate(r,kind);
            }
        }
    }
    if(goal==0)root=r;
}
void Insert(int k)//插入一个值为k的结点
{
    int r=root;
    if(r==0)
    {
        NewNode(root,0,k);
        return;
    }
    while(ch[r][key[r]<k])
    {
        r=ch[r][key[r]<k];
    }
    NewNode(ch[r][key[r]<k],r,k);
    Splay(ch[r][key[r]<k],0);
}
int Get_Min(int r)
{
    while(ch[r][0])
    {
        r=ch[r][0];
    }
    return r;
}
int Get_Max(int r)
{
    while(ch[r][1])
    {
        r=ch[r][1];
    }
    return r;
}
int main()
{
    int n;
    scanf("%d",&n);
    int num;
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(scanf("%d",&num)==EOF)num=0;
        Insert(num);
        if(i==1)
        {
            ans+=num;
        }
        else
        {
            int tmp=INF;
            if(ch[root][0])
                tmp=min(tmp,key[root]-key[Get_Max(ch[root][0])]);
            if(ch[root][1])
                tmp=min(tmp,key[Get_Min(ch[root][1])]-key[root]);
            ans+=tmp;
        }
    }
    printf("%d\n",ans);
    return 0;
}

3、HDU 1890 Robotic Sort（区间反转、删除根结点）

Robotic Sort

Time Limit: 6000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1403 Accepted Submission(s): 592

Problem Description

Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes.

In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.

Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.

A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.

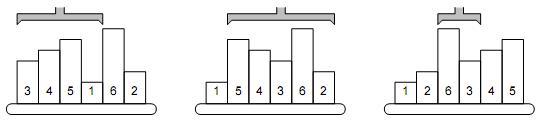
The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.

Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.

Input

The input consists of several scenarios. Each scenario is described by two lines. The first line contains one integer number N , the number of samples, 1 ≤ N ≤ 100 000. The second line lists exactly N space-separated positive integers, they specify the heights of individual samples and their initial order.

The last scenario is followed by a line containing zero.

Output

For each scenario, output one line with exactly N integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.

Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.

Sample Input

6 3 4 5 1 6 2 4 3 3 2 1 0

Sample Output

4 6 4 5 6 6 4 2 4 4

Source

2008 “Shun Yu Cup” Zhejiang Collegiate Programming Contest - Warm Up（2）

Recommend

linle

主要是想法比较好，反正和删除是很典型的操作了。

反转的splay时候一定要先push_down下去，再判断。

View Code

/*
 * HDU 1890 Robotic Sort
 * 这题就是对 n个不同的数的排序过程，通过旋转将第i到的数放在正确的位置，题目就是输出每次旋转前第i大的数的位置。
 * 这题的意思就是直接按照结点编号1-n建立一颗树。每个数代表初始位置的那个点，记录下每个数对应的点。
 * 每一次就是把第i大的数旋转到根结点。删除这个点然后旋转左区间。
 * 其实也可以用区间模拟，不删除的做法。
 * 操作有：反转、删除根结点
 * 需要的变量:pre,ch,size,rev;
 */
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
const int MAXN=100010;
int pre[MAXN],ch[MAXN][2],size[MAXN],rev[MAXN];
int root,tot1;
int n;
void NewNode(int &r,int father,int k)
{
    r=k;
    pre[r]=father;
    ch[r][0]=ch[r][1]=0;
    size[r]=1;
    rev[r]=0;
}
//反转的更新
void Update_Rev(int r)
{
    if(!r)return;
    swap(ch[r][0],ch[r][1]);
    rev[r]^=1;
}
void Push_Up(int r)
{
    size[r]=size[ch[r][0]]+size[ch[r][1]]+1;
}
void Push_Down(int r)
{
    if(rev[r])
    {
        Update_Rev(ch[r][0]);
        Update_Rev(ch[r][1]);
        rev[r]=0;
    }
}
void Build(int &x,int l,int r,int father)
{
    if(l>r)return;
    int mid=(l+r)/2;
    NewNode(x,father,mid);
    Build(ch[x][0],l,mid-1,x);
    Build(ch[x][1],mid+1,r,x);
    Push_Up(x);//这个不用忘记
}
void Init()
{
    root=tot1=0;
    ch[root][0]=ch[root][1]=size[root]=rev[root]=0;
    Build(root,1,n,0);
}
//旋转，基本固定
void Rotate(int x,int kind)
{
    int y=pre[x];
    Push_Down(y);
    Push_Down(x);
    ch[y][!kind]=ch[x][kind];
    pre[ch[x][kind]]=y;
    if(pre[y])
        ch[pre[y]][ch[pre[y]][1]==y]=x;
    pre[x]=pre[y];
    ch[x][kind]=y;
    pre[y]=x;
    Push_Up(y);
}
//Splay调整
void Splay(int r,int goal)
{
    Push_Down(r);
    while(pre[r]!=goal)
    {
        if(pre[pre[r]]==goal)
        {
            //这题有反转操作，需要先push_down,在判断左右孩子
            Push_Down(pre[r]);
            Push_Down(r);
            Rotate(r,ch[pre[r]][0]==r);
        }

        else
        {
            //这题有反转操作，需要先push_down,在判断左右孩子
            Push_Down(pre[pre[r]]);
            Push_Down(pre[r]);
            Push_Down(r);
            int y=pre[r];
            int kind=(ch[pre[y]][0]==y);
            //两个方向不同，则先左旋再右旋
            if(ch[y][kind]==r)
            {
                Rotate(r,!kind);
                Rotate(r,kind);
            }
            //两个方向相同，相同方向连续两次
            else
            {
                Rotate(y,kind);
                Rotate(r,kind);
            }
        }
    }
    Push_Up(r);
    if(goal==0)root=r;
}
int Get_Min(int r)
{
    Push_Down(r);
    while(ch[r][0])
    {
        r=ch[r][0];
        Push_Down(r);
    }
    return r;
}
int Get_Max(int r)
{
    Push_Down(r);
    while(ch[r][1])
    {
        r=ch[r][1];
        Push_Down(r);
    }
    return r;
}
//删除根结点
void Remove()
{
    if(ch[root][0]==0)//没有左孩子
    {
        root=ch[root][1];
        pre[root]=0;
    }
    else
    {
        int m=Get_Max(ch[root][0]);
        Splay(m,root);
        ch[m][1]=ch[root][1];
        pre[ch[root][1]]=m;
        root=m;
        pre[root]=0;
        Push_Up(root);//要更新
    }
}
struct Node
{
    int id,num;
}a[MAXN];
bool cmp(Node n1,Node n2)
{
    if(n1.num!=n2.num)return n1.num<n2.num;
    else return n1.id<n2.id;
}
int main()
{
    while(scanf("%d",&n)==1&&n)
    {
        Init();
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i].num);
            a[i].id=i;
        }
        sort(a+1,a+1+n,cmp);
        for(int i=1;i<n;i++)
        {
            Splay(a[i].id,0);
            Update_Rev(ch[root][0]);
            printf("%d ",i+size[ch[root][0]]);
            Remove();
        }
        printf("%d\n",n);
    }
    return 0;
}

Your friend, Jackson is invited to a TV show called SuperMemo in which the participant is told to play a memorizing game. At first, the host tells the participant a sequence of numbers, {A₁, A₂, ... A_n}. Then the host performs a series of operations and queries on the sequence which consists:

ADD x y D: Add D to each number in sub-sequence {A_x ... A_y}. For example, performing "ADD 2 4 1" on {1, 2, 3, 4, 5} results in {1, 3, 4, 5, 5}
REVERSE x y: reverse the sub-sequence {A_x ... A_y}. For example, performing "REVERSE 2 4" on {1, 2, 3, 4, 5} results in {1, 4, 3, 2, 5}
REVOLVE x y T: rotate sub-sequence {A_x ... A_y} T times. For example, performing "REVOLVE 2 4 2" on {1, 2, 3, 4, 5} results in {1, 3, 4, 2, 5}
INSERT x P: insert P after A_x. For example, performing "INSERT 2 4" on {1, 2, 3, 4, 5} results in {1, 2, 4, 3, 4, 5}
DELETE x: delete A_x. For example, performing "DELETE 2" on {1, 2, 3, 4, 5} results in {1, 3, 4, 5}
MIN x y: query the participant what is the minimum number in sub-sequence {A_x ... A_y}. For example, the correct answer to "MIN 2 4" on {1, 2, 3, 4, 5} is 2

To make the show more interesting, the participant is granted a chance to turn to someone else that means when Jackson feels difficult in answering a query he may call you for help. You task is to watch the TV show and write a program giving the correct answer to each query in order to assist Jackson whenever he calls.

The first line contains n (n ≤ 100000).

The following n lines describe the sequence.

Then follows M (M ≤ 100000), the numbers of operations and queries.

The following M lines describe the operations and queries.

For each "MIN" query, output the correct answer.

Time Limit: 5000MS		Memory Limit: 131072K
Total Submissions: 41977		Accepted: 12207
Case Time Limit: 2000MS

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 5839		Accepted: 1884
Case Time Limit: 2000MS

Splay Tree（伸展树总结）

Robotic Sort

Play with Chain

Queue-jumpers