无向图概念:(这里的x->y表示x和y之间有一条无向边)
1.桥:对于一个无向图,如果删除某条边后,该图的连通分量增加,则称这条边为桥
比如1->2->3->4这样一个简单得图一共有3个桥,分别是1->2,2->3,3->4
1->2->3->4->1 这样就没有桥,因为删除任意一个边,任意两点还可以互相往来(因为是双向边嘛)
2.割点/割项:对于一个无向图,如果删除某个节点u后,该图的连通分量增加,则节点u为割项或关节点
1->2->3->4 这样的图有2个割点,分别是2,3
1->2->3->4->1这样的图也是没有割点的,删除任意一个点其他点还是可以往来的
3.点-双联通:对于一个连通图,如果任意两点至少存在两条点不重复路径(即在从x走到y,如果删除任意一个其他点还可以从x走到y),
则称这个图为点双连通(也就是通常说的的双联通) 这样的图没有割点
4.边-双联通:对于一个连通图,如果任意两点至少存在两条边不重复路径,则称该图为边双连通的
这样的图没有割边
题意:
贝西和牛群被迫从一片标着1..F的牧场走到另一片牧场,他们必须在烂苹果树附近穿过。奶牛现在已经厌倦了经常被迫走一条特定的路,想要建一些新的路,这样它们就可以在任何一对田地之间至少有两条不同的路可选。他们目前在每对字段之间至少有一条路由,并且希望至少有两条路由。
题解:
那我们可以把所有割边都消除了就可以了
我们通过看图可以发现,割边一般是存在在一个点只与其他所有点有且仅有一条无向边
因为题目上已经保证了任意两点之间至少有一条路,所有我们找到所有这样的点,让它们互相连起来就可以了
黑边是原图的,红边是添加后使图变成边-双连通图的

根据上面描述,2,3,4都属于这样的点,我们就需要2条边就可以使它变成双连通图
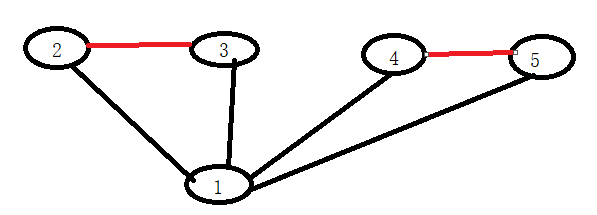
根据上面描述,2,3,4,5都属于这样的点,我们就需要2条边就可以使它变成双连通图
这样的话,任意一个点到达其他点至少有两条路径
代码1:

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 const int maxn=5010; 8 int head[maxn],cnt,num,stacks[maxn],top,cut,in[maxn],out[maxn]; 9 struct edge 10 { 11 int v,next; 12 }e[maxn]; 13 int visit[maxn],belong[maxn],dfn[maxn],low[maxn]; 14 void add_edge(int x,int y) 15 { 16 e[cnt].v=y; 17 e[cnt].next=head[x]; 18 head[x]=cnt++; 19 } 20 void init() 21 { 22 memset(in,0,sizeof(in)); 23 memset(out,0,sizeof(out)); 24 memset(head,-1,sizeof(head)); 25 cnt=num=top=cut=0; 26 } 27 void tarjan(int x,int pre) 28 { 29 low[x]=dfn[x]=++num; 30 visit[x]=1; 31 stacks[top++]=x; 32 int flag=1; 33 for(int i=head[x];i!=-1;i=e[i].next) 34 { 35 int v=e[i].v; 36 if(v==pre && flag) 37 { 38 flag=0; 39 continue; 40 } 41 if(!dfn[v]) 42 { 43 tarjan(v,x); 44 low[x]=min(low[x],low[v]); 45 } 46 else if(visit[v]) 47 { 48 low[x]=min(low[x],dfn[v]); 49 } 50 } 51 if(low[x]==dfn[x]) 52 { 53 cut++; 54 int v; 55 while(true) 56 { 57 v=stacks[top-1]; 58 top--; 59 belong[v]=cut; 60 visit[v]=0; 61 if(v==x) break; 62 //printf("*"); 63 } 64 } 65 } 66 int main() 67 { 68 int n,m; 69 init(); 70 scanf("%d%d",&n,&m); 71 while(m--) 72 { 73 int x,y; 74 scanf("%d%d",&x,&y); 75 add_edge(x,y); 76 add_edge(y,x); 77 } 78 tarjan(1,-1); 79 //printf("** "); 80 for(int i=1;i<=n;++i) 81 { 82 for(int j=head[i];j!=-1;j=e[j].next) 83 { 84 int v=e[j].v; 85 if(belong[i]!=belong[v]) 86 { 87 in[belong[v]]++; 88 out[belong[i]]++; 89 } 90 } 91 } 92 int ans=0; 93 for(int i=1;i<=n;++i) 94 { 95 if(out[i]==1) 96 ans++; 97 } 98 printf("%d ",(ans+1)/2); 99 }
代码2:

1 //time 1031MS 2 3 //memory 31340K 4 5 #pragma comment(linker, "/STACK:1024000000,1024000000") 6 7 #include <iostream> 8 9 #include <cstdio> 10 11 #include <cstdlib> 12 13 #include <cstring> 14 15 #define MAXN 300015 16 17 #define MAXM 4000015 18 19 using namespace std; 20 21 struct Edge{ 22 23 int v,next; 24 25 }e[MAXM]; 26 27 int head[MAXN],en; 28 29 int head2[MAXN],en2; 30 31 int belong[MAXN],dfn[MAXN],low[MAXN],sta[MAXN],top,num,scc; 32 33 int in[MAXN],out[MAXN]; 34 35 bool vis[MAXN]; 36 37 void init() 38 39 { 40 41 memset(head,-1,sizeof(head)); 42 43 memset(vis,0,sizeof(vis)); 44 45 en = 0; 46 47 top = 0; 48 49 scc=num = 0;memset(dfn,0,sizeof(dfn)); 50 51 } 52 53 void addedge(int u,int v) 54 55 { 56 57 e[en].v = v; 58 59 e[en].next = head[u]; 60 61 head[u] = en++; 62 63 } 64 65 //void addedge2(int u,int v) 66 // 67 //{ 68 // 69 // edge2[en2].v = v; 70 // 71 // edge2[en2].next = head2[u]; 72 // 73 // head2[u] = en2++; 74 // 75 //} 76 77 void tarjan(int u,int fa) 78 79 { 80 81 dfn[u] = low[u] = ++num; 82 83 sta[++top] = u; 84 85 int cnt=0; 86 87 for(int i = head[u]; i != -1; i = e[i].next) 88 89 { 90 91 int v = e[i].v; 92 93 if(!dfn[v]) 94 95 { 96 97 tarjan(v,u); 98 99 low[u] = min(low[u],low[v]); 100 101 } 102 103 else if (fa==v) 104 105 { 106 107 if (cnt) low[u] = min(low[u],dfn[v]);//重边 108 109 cnt++; 110 111 } 112 113 else low[u] = min(low[u],dfn[v]); 114 115 } 116 117 if(dfn[u]==low[u]) 118 119 { 120 121 int x; 122 123 scc++; 124 125 do 126 127 { 128 129 x = sta[top--]; 130 131 belong[x] = scc; 132 133 }while(x!=u); 134 135 } 136 137 } 138 139 //void build() 140 // 141 //{ 142 // 143 // en2 = 0; 144 // 145 // memset(head2,-1,sizeof(head2)); 146 // 147 // for(int i = 1; i <= n; i++) 148 // 149 // { 150 // 151 // for(int j = head[i]; j!=-1; j = e[j].next) 152 // 153 // { 154 // 155 // int v = e[j].v; 156 // 157 // if(belong[i]!=belong[v]) 158 // 159 // addedge2(belong[i],belong[v]); 160 // 161 // } 162 // 163 // } 164 // 165 //} 166 167 int ans; 168 169 //int dfs(int u,int p) 170 // 171 //{ 172 // 173 // int max1=0,max2=0; 174 // 175 // for (int i=head2[u];i!=-1;i=edge2[i].next) 176 // 177 // { 178 // 179 // int v=edge2[i].v; 180 // 181 // if (v==p) continue; 182 // 183 // int tmp=dfs(v,u)+1; 184 // 185 // if (max1<tmp) max2=max1,max1=tmp; 186 // 187 // else if (max2<tmp) max2=tmp; 188 // 189 // } 190 // 191 // ans=max(ans,max1+max2); 192 // 193 // return max1; 194 // 195 //} 196 int main() 197 { 198 int n,m; 199 init(); 200 scanf("%d%d",&n,&m); 201 while(m--) 202 { 203 int x,y; 204 scanf("%d%d",&x,&y); 205 addedge(x,y); 206 addedge(y,x); 207 } 208 tarjan(1,-1); 209 //printf("** "); 210 for(int i=1;i<=n;++i) 211 { 212 for(int j=head[i];j!=-1;j=e[j].next) 213 { 214 int v=e[j].v; 215 if(belong[i]!=belong[v]) 216 { 217 in[belong[v]]++; 218 out[belong[i]]++; 219 } 220 } 221 } 222 int ans=0; 223 for(int i=1;i<=n;++i) 224 { 225 if(out[i]==1) 226 ans++; 227 } 228 printf("%d ",(ans+1)/2); 229 } 230 //int main() 231 // 232 //{ 233 // 234 // //freopen("/home/qitaishui/code/in.txt","r",stdin); 235 // 236 // int u,v; 237 // 238 // while(scanf("%d%d",&n,&m)&&(n+m)) 239 // 240 // { 241 // 242 // init(); 243 // 244 // //cout<<n<<m<<endl; 245 // 246 // for(int i = 0; i < m; i++) 247 // 248 // { 249 // 250 // scanf("%d%d",&u,&v); 251 // 252 // if (v==u) continue; 253 // 254 // addedge(u,v); 255 // 256 // addedge(v,u); 257 // 258 // //cout<<u<<" "<<v<<endl; 259 // 260 // } 261 // 262 // 263 // 264 // tarjan(1,-1); 265 // 266 // build(); 267 // 268 // ans=0; 269 // 270 // dfs(1,-1); 271 // 272 // printf("%d ",scc-ans-1); 273 // 274 // } 275 // 276 // return 0; 277 // 278 //}
