二叉树
Content
二叉树用途
二叉树结构
二叉树分类
二叉树建立
二叉树遍历
二叉树用途
二叉树应用非常广泛。首先二叉树是树的基础zhi,利用二叉树可以构造树和森林。在操作系统源程序中,树和森林被用来构造文件系统。我们看到的window和linux等文件管理系统都是树型结构。在编译系统中,如C编译器源代码中,二叉树的中序遍历形式被用来存放C 语言中的表达式。在游戏设计领域,许多棋类游戏的步骤都是按树型结构编写。其次二叉树本身的应用也非常多,如哈夫曼二叉树用于JPEG编解码系统(压缩与解压缩过程)的源代码中,甚至于编写处理器的指令也可以用二叉树构成变长指令系统,另外二叉排序树被用于数据的排序。(摘自百度)
二叉树结构
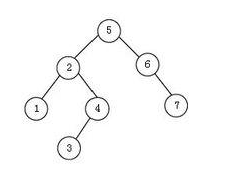
二叉树相关概念:根、父节点、左子树、右子树、节点度数、树层数、树高度
- 根:如图中5所在位置即为根,一棵二叉树只有一个根
- 左子树:以一个节点的左节点为根,以下的所有元素构成左子树(右子树同理)
- 节点度数:二叉树结点的度数指该结点所含子树的个数
- 树高度:树的高度等于所有节点的最大深度(即树的深度),二叉树的深度是指所有结点中最深的结点所在的层数
二叉树分类
完全二叉树、满二叉树、平衡二叉树……
1. 完全二叉树
若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子结点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。

2. 满二叉树
对于国内的满二叉树:从图形形态上看,满二叉树外观上是一个三角形
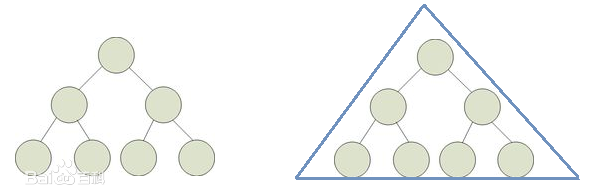
对于国外的满二叉树:满二叉树的结点要么是叶子结点,度为0,要么是度为2的结点,不存在度为1的结点
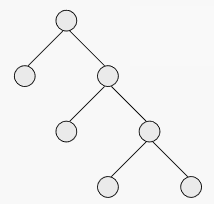
(来源百度)
二叉树建立
一、二叉树的数据存储结构
二叉树是通过结构体里嵌套结构体,不断连续,图解结构如下
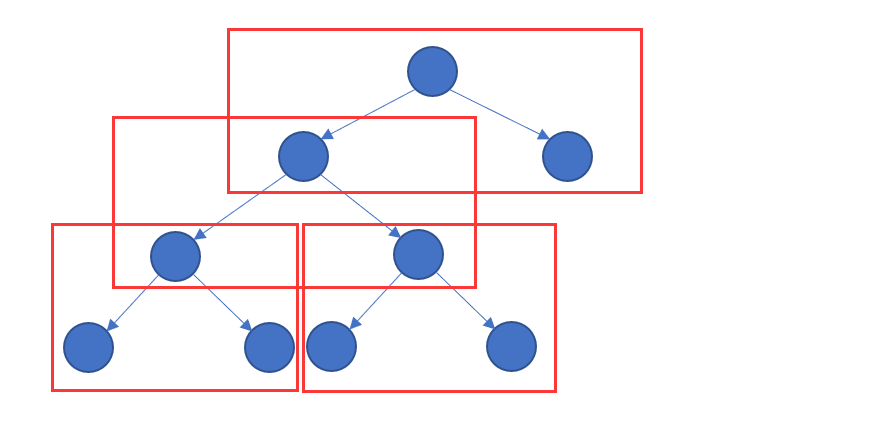
一个红框代表一个结构体,而整个结构体即使一棵树
二、树的建立
二叉树遍历
前序遍历、中序遍历、后序遍历
视频讲解链接(讲得还不错)https://www.bilibili.com/video/BV16b411h7PH?from=search&seid=17078682895324345600
前序遍历可行代码
口诀:根-左-右(仅看单个最小单元结构体)
void PreOrderTraverse(BTreeNode *ptree, int level)
{
if (ptree == NULL)
return;
cout << ptree->data << "在第" << level++ << "层" << endl;
PreOrderTraverse(ptree->lchild, level);
PreOrderTraverse(ptree->rchild, level);
}
中序遍历可行代码
口诀:左-根-右
void PreOrderTraverse(BTreeNode *ptree, int level) { if (ptree == NULL) return; cout << ptree->data << "在第" << level++ << "层" << endl; PreOrderTraverse(ptree->lchild, level); PreOrderTraverse(ptree->rchild, level); }
后序遍历可行代码
口诀:左-右-根
void PreOrderTraverse(BTreeNode *ptree, int level)
{
if (ptree == NULL)
return;
PreOrderTraverse(ptree->lchild, level);
PreOrderTraverse(ptree->rchild, level);
cout << ptree->data << endl;
}
写在最后
二叉树的建立和遍历,都是涉及到递归知识,代码也许比较简单,但是其运行过程却相对比较复杂,不易理解。二叉树初学,代码理解不是很透彻,欢迎指正,欢迎来和Kirk讨论研究,我们一起进步哦!
最后奉上完整的代码
1 #include <iostream> 2 #include <stdlib.h> 3 using namespace std; 4 5 void CreatBiTree(BTreeNode *&ptree); // 建树函数 6 void PreOrderTraverse(BTreeNode *ptree, int level); // 遍历树 7 8 struct BTreeNode 9 { 10 int data = 0; // 节点信息 11 BTreeNode *lchild; // 左节点 12 BTreeNode *rchild; // 右节点 13 }; 14 15 void CreatBiTree(BTreeNode *&ptree) 16 { 17 char character; 18 cin >> character; // 输入节点信息,以NULL标志该节点无信息并结束节点停止延申 19 if (character == '#') 20 ptree = NULL; 21 else 22 { 23 ptree = new BTreeNode; // 给新的左右节点申请空间 24 ptree->data = character; // 录入当前节点信息 25 CreatBiTree(ptree->lchild); // 递归调用 26 CreatBiTree(ptree->rchild); 27 } 28 return; 29 } 30 31 void PreOrderTraverse(BTreeNode *ptree, int level) 32 { 33 if (ptree == NULL) 34 return; 35 cout << ptree->data << "在第" << level++ << "层" << endl; 36 PreOrderTraverse(ptree->lchild, level); 37 PreOrderTraverse(ptree->rchild, level); 38 } 39 40 int main() 41 { 42 BTreeNode *root = NULL; 43 CreatBiTree(root); 44 int level = 0; 45 PreOrderTraverse(root, level); 46 return 0; 47 }