素数算法总结
Content
一. 经典算法
素数定义算法
素数定义算法升级
二. 进阶算法
(一)埃氏筛
(二)欧拉筛
写在最后
一.经典算法
素数定义:
只能被1和他本省整除数
依据定义可以使用最为暴力的方法 —— 判定1到该数的中间是否存在可整除该数的数
代码
1 bool isPrime(int n) //素数判断函数 2 3 { 4 int i; 5 for (i = 2; i <= n; ++i) 6 { 7 if (n % i == 0) 8 break; 9 } 10 if (i == n) 11 return 1; 12 else 13 return 0; 14}
当然,此代码可以优化一下:
1 bool isPrime(int n) 2 { 3 for (int i = 2; i <= sqrt(n); i++) 4 { 5 if (n % i == 0) 6 return false; 7 } 8 return true; 9 }
注:这两函数以返回值来表示该数是不是素数,1为素数、0为合数(0、1除外)。
二. 素数进阶算法
(一) 埃拉托斯特尼筛法(埃氏筛)
时间复杂度:O(n*loglogn)
核心思想:
从小到大,用一个数组的角标表示一个数,数组内储存的值为标记,用小的素数的倍数来筛出较大的合数,将范围内的合数和质素分别标记从而获得一张素数表
例如:寻找20以内的质数
1和2直接标记;读到2的时候标记2*2、2*3、2*4、2*5、5*6、2*7、2*8、2*9、2*10;所以数组vis[1] == 0、vis[2] == 1、vis[3] == 1、vis[2*2] == 0 .......
为了进一步节省算力,我们不必将读到20才结束循环,只需要读到sqrt(20)就行
可行代码:
1 const int N = 100000000; 2 bool vis[N]; 3 void sieve(int n) 4 5 { 6 int m = (int)sqrt(n + 0.5); 7 memset(vis, 0, sizeof(vis));//初始化数组,此函数在<string.h>内 8 vis[2] = 0; 9 for (int i = 3; i <= m; i += 2) { 10 if(!vis[i]) 11 for (int j = i * i && i * i < n; j <= n; j += i) 12 vis[j] = 1; 13 } 14 }
(二) 欧拉筛(线性筛)
时间复杂度O(n)
埃氏筛对于处理1E7以下的数据比较友好,一旦数据过大埃氏筛也很难跑出结果,对埃氏筛进一步优化就可以得到欧拉筛。在埃氏筛的筛除过程中会出现重复筛除,例如:100会被2*50、4*25、5*20、10*10同时筛掉,欧拉筛就会让每一个数只被筛除一次,在大数据进行运算的时候会导致一个较大的数同时被筛除很多次,欧拉筛就可以解决这个问题,我们需要让一个数只被他的最大质因数筛除即可达到目的。
1 const int N = 10000000; 2 int prime[N]; //储存素数 3 bool vis[N]; //制作素数表格 4 int cnt = 0; 5 void ouler_srcreen() 6 { 7 memset(vis, true, N); 8 vis[0] = vis[1] = false; //初始化 9 for (int i = 2; i <= N; i++) 10 { 11 if (vis[i]) 12 prime[cnt++] = i; //判断出i为素数就将素数出入数组 13 for (int j = 0; j <= cnt && prime[j] * i <= N; j++) 14 { 15 vis[i * prime[j]] = false; //标记非素数 16 if (i % prime[j] == 0) 17 break; //欧拉筛核心,避免重复筛选 18 } 19 } 20 return; 21 }
两筛对比:

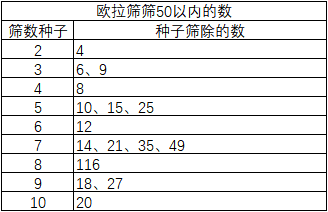
注:此代码以vis数组为表格,vis的角标值为实际的数,vis所储存的值为判断角标所代表的数是否为素数,1为素数、0为合数(0、1除外)。
写在最后
简单的从定义入手会比较好理解,对于定义筛法的第二种升级版本之需要遍历到该数开平方的位置这个kirk还没了解数学上的证明方法,欢迎感兴趣的读者来与kirk交流啊。
对于埃氏筛和欧拉筛,旨在理解其筛数的核心思想,利用倍数巧妙剔除多余的合数,为了避免重复筛除带来的算力浪费,欧拉筛站出来解决了重复筛除的浪费。
本文也许有些地方读者不懂的话,欢迎留言,Kirk也欢迎你来询问。文中若有什么纰漏,还请各位读者谅解并及时联系修改,谢谢咯