图卷积神经网络

图卷积神经网络

现实世界许多数据都是以graph的形式存储的，比如social networks(社交网络),knowledge graphs(知识图谱),最近有一些研究者把目光投向建立一种通用的神经网络模型处理graph数据。

图上的卷积网络从卷积方式上可以分为两种：1.谱（spectral）卷积，2.空间域卷积。谱卷积将卷积网络的滤波器与图信号同时搬移到傅里叶域以后进行处理。而空间域的卷积，让图中的节点在空间域中相连、达成层级结构，进而进行卷积。

谱图卷积

空间卷积

 

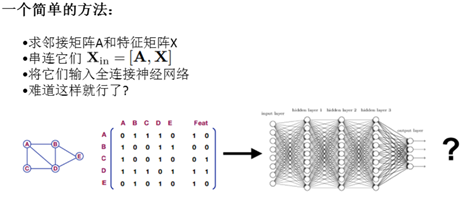
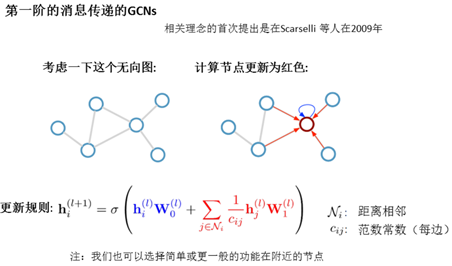
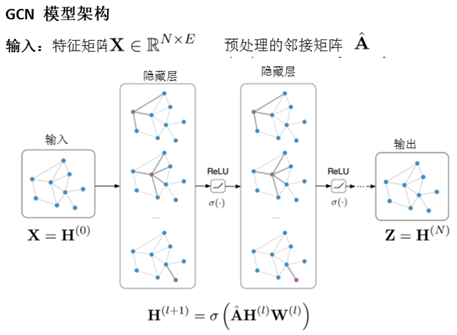
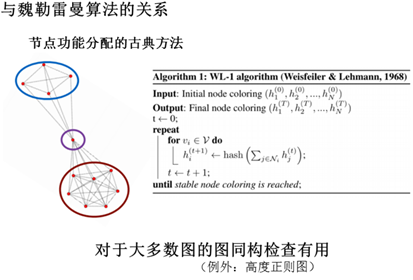
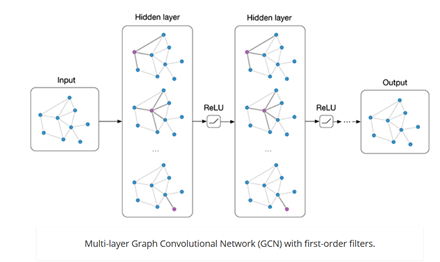
由于大家的思想普遍是如何将CNN等神经网络的思想迁移到graph上，所以往往设计出来的结构都有一定的共性，使用类似convolution权重共享的思想，我们可以把这类网络暂且称为Graph Convolutional Networks(GCNs)。这类网络从数学上来看，是想学习G=(V,E)上的一个函数，该函数的输入是：

• 每一个节点的特征表示,如果节点数为N，特征维度为D维，则所有节点的特征组成一个的矩阵
• 图结构的表达，往往使用图的邻接矩阵A表示

该函数产生一个node-level的输出Z（是一个的矩阵，N代表点数量，每一行代表一个节点，F代表节点特征向量的维度）。如果想要得到graph-level的特征表达，只需要将每一个node的表达综合起来再经过一个映射操作即可。

和卷积神经网络一样，对于graph的特征提取我们同样可以使用多层神经网络结构，对于每一层，我们可以使用如下的映射函数来计算：

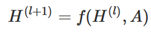
,X是图的输入，Z是图的输出，L是模型的层数。表示第l层graph的node-level表达，是一个维的矩阵，N代表node数量，代表第l层节点表达的维度（节点表达的维度可以在每一层都不一样，由f决定可以灵活设置）；

对于层间的映射函数f，我们可以采用如下式的方式实现：

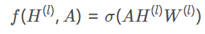
其中,,,是非线性激活函数。这里简单解释一下这么做的物理意义，邻接矩阵与相乘的作用是使节点的邻接节点值求和聚集到该节点上，为了不丢失该节点本来信息，我们往往会强制每一个节点到自己也有一个连接，即一个self-loop，相当于让邻接矩阵A加上一个单位矩阵I，则上式变成如下形式

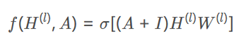
不过我们还可以对模型进行更近一个的改进。邻接矩阵并没有归一化，这样会导致每经过一次相乘节点特征的尺度就会变大，这样我们可以进一步将公式变为如下形式：

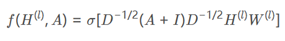
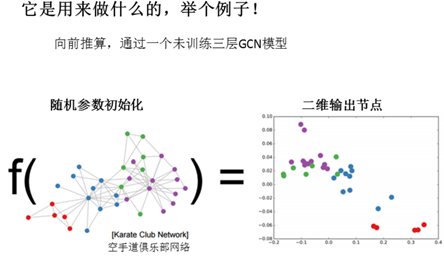
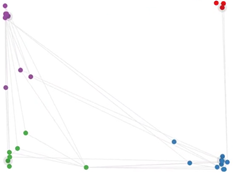
利用上面介绍的模型实现一个分类问题。数据集可以以下图的形式呈现，简单介绍的话就是说一个空手道俱乐部内部出现矛盾要被拆分为两波人，我们需要依据队员们平时的交往关系来判断他们会站哪一支队伍，图中每个节点表示一个队员，若两个节点之间存在边，则表示对应两个队员之间关系密切。

结果如下

GCN模型同样具备深度学习的三种性质：

1. 层级结构（特征一层一层抽取，一层比一层更抽象，更高级）
2. 非线性变换（增加模型的表达能力）
3. 端对端训练（不需要再去定义任何规则，只需给图的节点一个标记，让模型自己学习，融合特征信息和结构信息）

GCN四个特征：

1. GCN是对卷积神经网络在graph domain上的自然推广。
2. 它能同时对节点特征信息与结构信息进行端对端学习，是目前对图数据学习任务的最佳选择。
3. 图卷积适用性极广，适用于任何拓扑结构的节点与图。
4. 在节点分类与边预测等任务上，在公开数据集上效果远远优于其他方法。