三分法求解凸函数的最值
二分法作为分治中最常见的方法,适用于单调函数,逼近求解某点的值。但当函数是凸性函数时,二分法就无法适用,这时三分法就可以“大显身手”
函数必须严格单调递减
对于如下图的一个凸函数 $ f(x),x∈[left,right] (其中 lm 和 rm 分别为区间[left,right]的三等分点,我们发现如果) f(lm)<f(rm) $,那么函数值最小的点的横坐标x一定在[left,rm]之间。 同理,当f(lm)>f(rm)时,最值的横坐标x一定在[lm,right]的区间内。
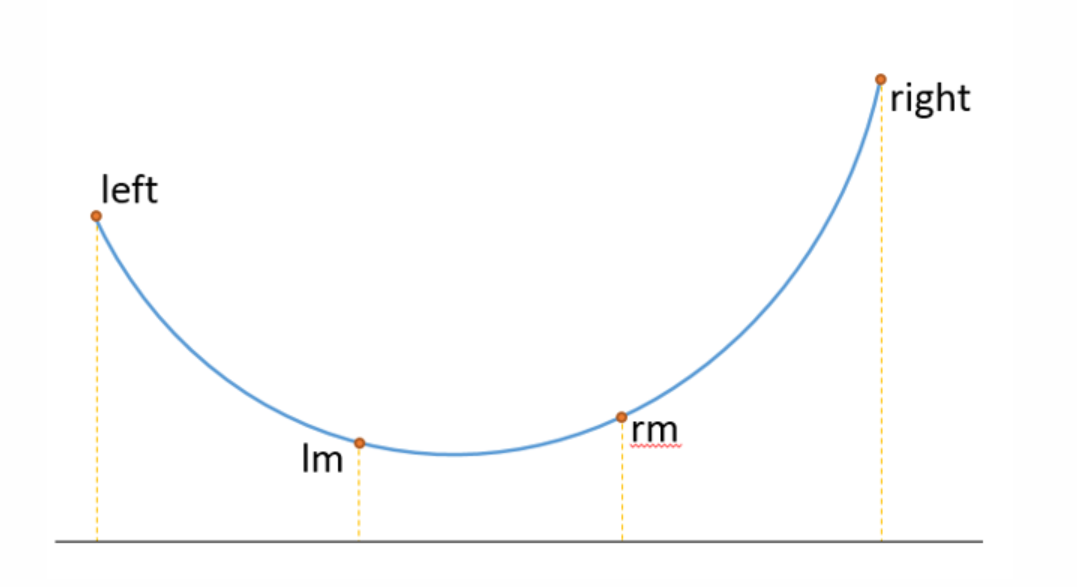
利用这个性质,我们就可以在缩小区间的同时向目标点逼近,从而得到极值。
while(r-l > 0.000...1)
题目若要保留x位就小数点后x个0
也可写成 1e-(x+1)
模板
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#define db double
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const db eps=1e-6;
int n;
db l,r,a[15],ans;
db qpow(db a,int b){
db res=1;
while(b){
if(b&1) res*=a;
a*=a;
b>>=1;
}
return res;
}
db get(db x) {
db res=0;
for(int i=0;i<=n;i++)
res+=qpow(x,i)*a[i];
return res;
}
int main() {
scanf("%d",&n);
scanf("%lf%lf",&l,&r);
for(int i=n;i;i--)
scanf("%lf",&a[i]);
while(r-l>eps){
db lm=l+(r-l)/3;
db rm=r-(r-l)/3;
get(lm)>get(rm)?r=rm,ans=lm:l=lm,ans=rm;
}
printf("%.5lf
",ans);
return 0;
}
模板2
我们令pivot代表抛物线的对称抽,可以发现当X>pivot,我们可以取left = pivot,right = inf, 反之left = -inf , right = pivot, 其距离恰好满足凸形函数。而我们要求的最短距离d,正好就是这个凸形函数的极值。
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double MAX = 100000;
double a,b,c,x,y;
double pivot;
double dis(double x_){
double y_=a*x_*x_+b*x_+c;
return sqrt((x-x_)*(x-x_)+(y-y_)*(y-y_));
}
double solve(double l,double r){
double lm=l+(r-l)/3;
double rm=r-(r-l)/3;
double lmd=dis(lm);
double rmd=dis(rm);
if(fabs(lmd-rmd)<0.0001) return lmd;
if(lmd>rmd) return solve(lm,r);
else return solve(l,rm);
}
int main(){
while(scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&x,&y)!=EOF){
pivot=-b/(2*a);
double l=0,r=0;
if(pivot<x){
l=pivot+0.0001;
r=MAX;
}else{
l=-MAX;
r=pivot-0.0001;
}
printf("%.3lf
",solve(l,r));
}
return 0;
}
https://blog.csdn.net/controlbear/article/details/54237388
咆咆咆哮
Solution
https://www.cnblogs.com/chenxiaoran666/p/CometOJDay4Div1I.html
fuc...拍了一上午都没拍出来。。。就是wa
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n;
int a[100005],b[100005],s[100005];
inline void Max(long long &x,long long y){if(x<y) x=y;}
inline long long get(int x){
long long res=0;
for(int i=1;i<=n;i++)
res+=a[i],s[i]=(1ll)*b[i]*x-a[i];
sort(s+1,s+1+n);
reverse(s+1,s+1+n);
for(int i=1;i<=n-x;i++) res+=s[i];
return res;
}
inline long long solve(int l,int r){
long long res=0;
while(r-l>2){
int lm=l+(r-l)/3,rm=r-(r-l)/3;
get(lm)>get(rm)?r=rm:l=lm;
}
for(int i=l;i<=r;i++)
Max(res,get(i));
return res;
}
int main(){
n=read();
for(int i=1;i<=n;i++)
a[i]=read(),b[i]=read();
printf("%lld
",solve(1,n));
return 0;
}
std
#include <bits/stdc++.h>
#define Reg register
#define RI Reg int
#define Con const
#define CI Con int &
#define I inline
#define N 100000
#define LL long long
#define Gmax(x, y) (x < (y) && (x = (y)))
using namespace std;
int n, a[N + 5], b[N + 5];
LL s[N + 5];
inline int read()
{
int x = 0, f = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
f = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
I LL GetAns(CI x) //求出在使用a[i]的卡牌张数为x时的最优答案
{
RI i;
Reg LL res = 0;
for (i = 1; i <= n; ++i)
res += a[i], s[i] = 1LL * b[i] * x - a[i]; //初始化答案
for (sort(s + 1, s + n + 1), i = n; i ^ x; --i)
res += s[i];
return res; //排序+贪心,返回答案
}
I LL Solve(RI l, RI r) //三分
{
RI i, lm, rm;
Reg LL res = 0;
while (r - l > 2)
{
lm = l + (r - l) / 3, rm = r - (r - l) / 3;
GetAns(lm) > GetAns(rm) ? r = rm : l = lm;
}
for (i = l; i <= r; ++i)
Gmax(res, GetAns(i));
return res;
}
int main()
{
n = read();
for (int i = 1; i <= n; ++i)
a[i] = read(), b[i] = read();
printf("%lld", Solve(1, n));
return 0;
}