目录:
·题目描述
·知识拓展
·题目分析
·思路分析
·代码实现
·总结
·题目描述:
我们可以把由“0”和“1”组成的字符串分为三类:全“0”串称为B串,全“1”串称为I串,既含“0”又含“1”的串则称为F串。
FBI树是一种二叉树,它的结点类型也包括F结点,B结点和I结点三种。由一个长度为2^N的“01”串S可以构造出一棵FBI树T,递归的构造方法如下:
1) T的根结点为R,其类型与串S的类型相同;
2) 若串S的长度大于1,将串S从中间分开,分为等长的左右子串S1和S2;由左子串S1构造R的左子树T1,由右子串S2构造R的右子树T2。
现在给定一个长度为2^N的“01”串,请用上述构造方法构造出一棵FBI树,并输出它的后序遍历序列。
·知识拓展:
关于遍历的顺序:
(1)先序遍历:
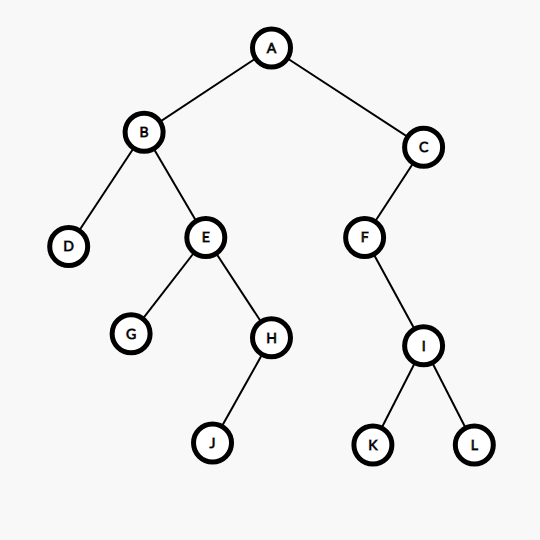
如图,这是一个二叉树,A为根结点。这张图如果用先序遍历表示的话,应为ABDEGHJCFIKL。总的来说,先序遍历的遍历方式为先根后左再右,简记为:根左右
(2)中序遍历:
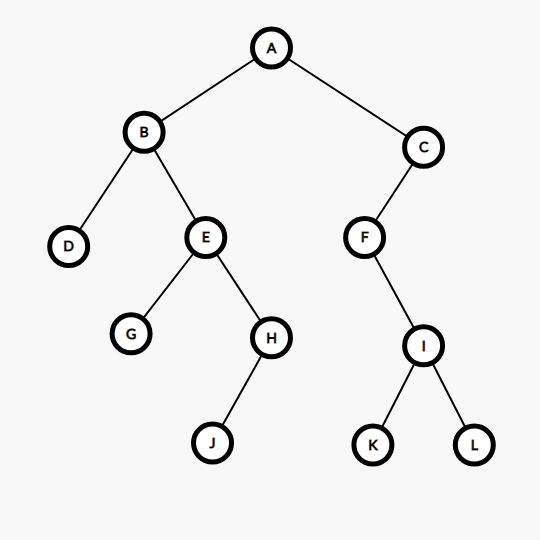
如图,还是这个二叉树,但是这张图如果用中序遍历表示的话,应为DBGEJHAFIKLC。不难看出,后序遍历的遍历方式为先左后根再右,简记为:左根右
(3)后序遍历:
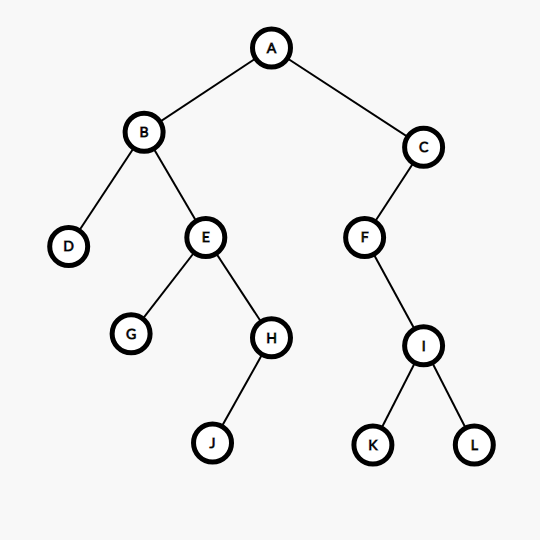
又是这张图,还是这个二叉树,用后序遍历表示这张图的话,应为DGJHEBKLIFCA。与上面的两种遍历方式相比较,可知,后序遍历的遍历方式为先左后右再根,简记为:左右根
·题目分析:
刚拿到这道题时,我没有仔细读题,只是将样例中的字符串写成了树,然后又按照后序遍历将这个字符串重新排列,将排列之后的字符串两个一组判断是F、B或I,但是这明显是错的。
本题的意思是将字符串写成树后,对每一个结点先进行判断F、B或I,然后按照后序遍历输出,没有对字符串长度的限制,不能两个一组进行判断
·思路分析:
对于这道题,我们可以采用边建树边输出的方法,结合深搜(其实就是一个大大的暴力),就可以得到这个题目的大致思路:
我们可以设一个dfs(l,r)函数,这个函数表示从l到r的字符串建树(并且输出F、B、I)
如果r-l>1,就将这个函数变为dfs(l,mid)和dfs(mid+1,r),其中mid为l和r的中点,就是(l+r)/2
如果r-l=1,这个函数就递归到了尽头,则需要按照后序遍历的方式将F、B、I输出
·代码实现:
好了,talk is cheap,show me the code
1 #include<iostream> 2 #include<string> 3 using namespace std; 4 int n; 5 string s; 6 void dfs(int l,int r){ 7 if(l==r){ 8 if(s[l]=='0')cout<<'B'; 9 if(s[l]=='1')cout<<'I'; 10 return ; 11 } 12 int mid=(l+r)/2; 13 dfs(l,mid); 14 dfs(mid+1,r);//后序遍历 15 bool B=true;//全是0 16 bool I=true;//全是1 17 for(int i=l;i<=r;i++){ 18 if(s[i]=='1')B=false;//有1 19 if(s[i]=='0')I=false;//有0 20 } 21 if(B)cout<<'B'; 22 else if(I)cout<<'I'; 23 else cout<<'F'; 24 } 25 int main(){ 26 cin>>n>>s;//用cin会好一点TwT 27 dfs(0,(1<<n)-1);//0~2^n-1 28 }
·总结:
这道题属于典型的“挂羊头卖狗肉”问题,题目名称和题目中的各个方面都是跟树相关,但是这个题目的解决方法却与树并没有太大的关系(虽然也用到了树的知识)。虽然自己图论学的不够好,但也不能因为题目中的暗示放弃了解题的机会啊!