题目连接:
https://www.acwing.com/problem/content/1317/
Description
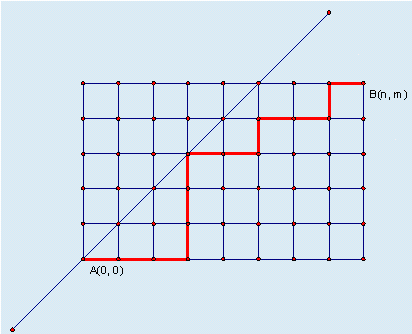
某城市的街道呈网格状,左下角坐标为 A(0,0),右上角坐标为 B(n,m),其中 n≥m。
现在从 A(0,0) 点出发,只能沿着街道向正右方或者正上方行走,且不能经过图示中直线左上方的点,即任何途径的点 (x,y) 都要满足 x≥y,请问在这些前提下,到达 B(n,m) 有多少种走法。
Input
仅有一行,包含两个整数 n 和 m,表示城市街区的规模。
(1≤m≤n≤5000)
Output
输出一个整数,表示不同的方案总数。
Sample Input
6 6
Sample Output
132
题解
可以利用卡特兰数的这条性质:卡特兰数 Catalan number。得到(n,m)关于红线的对称点:先将所有下移一格:(n,m-1),红线过(0,0),得到对称点:(m-1,n),再上移一格对称点最终:(m-1,n+1)。答案为C(n+m,m)-C(n+m,m-1)。
首先求精确值,需要用到高精度,n,m比较大,需要枚举阶层质因子来求。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int st[N],prime[N],tot,sum[N],a[N],b[N],ans[N];
void get_Prime(){
for(int i=2;i<N;++i){
if(!st[i]) prime[++tot]=i;
for(int j=1;prime[j]<=N/i;++j){
st[prime[j]*i]=1;
if(!(i%prime[j])) break;
}
}
}
int calc(int x,int y){
int cnt=0;
while(x){
cnt+=x/y;
x/=y;
}
return cnt;
}
void mul(int arr[],int b){
for(int i=0;i<N;++i){
arr[i]*=b;
if(i>0)
arr[i]+=arr[i-1]/10,arr[i-1]%=10;
}
}
void solve(int arr[],int a,int b){
for(int i=1;i<=tot;++i){
int p=prime[i];
sum[i]=calc(a,p)-calc(b,p)-calc(a-b,p);
}
arr[0]=1;
for(int i=1;i<=tot;++i){
for(int j=1;j<=sum[i];++j){
mul(arr,prime[i]);
}
}
}
void print(int arr[]){
int i=N-1;
while(arr[i]==0&&i>=0) --i;
while(i>=0) cout<<arr[i--];
puts("");
}
int main(){
get_Prime();
int n,m;
cin>>n>>m;
solve(a,n+m,n);
solve(b,n+m,m-1);
for(int i=0;i<N;++i){
ans[i]+=a[i]-b[i];
if(ans[i]<0) ans[i+1]--,ans[i]+=10;
}
print(ans);
return 0;
}