4.2基本概念
1、傅里叶正反变换的理解 https://www.cnblogs.com/jingxin-gewu/p/13535848.html
2、卷积,时域的卷积和频率域的乘积是一对傅里叶变换对,时域的乘积和频域的卷积是傅里叶变换对
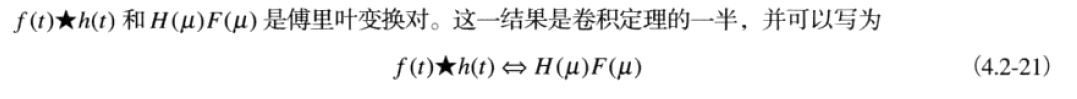
![]()
4.3取样
1、一个函数乘一个冲击串就是对这个函数取了样,取样函数的傅里叶变换是由原函数傅里叶变换的副本组成,要想取样后的函数能够恢复,就需要满足这些副本不会重叠,也就是满足取样定律:
取样频率需要超过函数最高频率的两倍,下图的图b、图c满足取样定理,图d不满足取样定理,产生了混淆。

实际上,混淆是无法避免的,因为通常被取样的函数都是一个时间有限的函数,他的频率域可以扩展到无穷大(p136),我们无法找到一个符合采样定理的采样频率
4.6空间域与频率域的一些关系(p156)
1、图像的平移不影响谱而影响相角
2、图像的旋转会影响谱
3、相角支配图像的形状
4.7频率域滤波基础
1、低频对应变化缓慢,高频对应变化剧烈
2、频率域处理时要注意对图像在空间域进行填充
3、空间域卷积和频率域相乘对应
4.8频率域滤波平滑图像(低通滤波)
1、理想低通,频率域是盒状函数,映射到空间域会存在振铃现象
2、布斯特沃低通滤波在低通滤波效果和振铃现象之间进行了较好折中
3、高斯低通滤波,完全不存在振铃现象
4.9频率域滤波锐化图像(高通滤波)
1、用1减去低通滤波就得到高通滤波
2、有理想高通、布斯特沃、高斯三种高通滤波器
3、频率域的拉普拉斯算子也可用于锐化图像
4、高频强调滤波
5、同态滤波适用于照射-反射模型
4.10选择性滤波
阻止或者通过特定频率,实现降噪等效果
4.11实现
FFT算法可以极大地加快运算速度