[算法题] 汉诺塔问题

问题描述
三个柱子，起初有若干个按大小关系顺序安放的盘子，需要全部移动到另外一个柱子上。移动规则：在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
移动次数： f(n)=2n -1

解法思路

使用递归算法进行处理。

汉诺塔的算法大概有3个步骤：

（1）把a上的n-1个盘通过c移动到b。

（2）把a上的最下面的盘移到c。

（3）因为n-1个盘全在b上了，所以把b当做a重复以上步骤就好了。

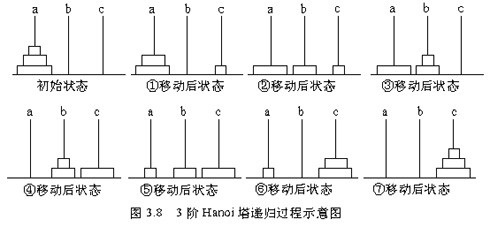
在网上找到一个3阶的汉诺塔递归过程示意图，参考一下。

代码实现

代码

#include <stdio.h>

int step = 0;
void hanoi(int n, char start, char assist, char end){
    if(n>=1){
        hanoi(n-1, start, end, assist);
        printf("move %d from %c --> %c 
", n, start, end);
        step++;
        hanoi(n-1, assist, start, end);
    }
}

int main(){
    int n;
    scanf("%d", &n);
    hanoi(n, 'A', 'B', 'C');
    printf("Totally move %d steps
", step);
    return 0;
}

运行结果

Please input the disk num:
3
move 1 from A --> C
move 2 from A --> B
move 1 from C --> B
move 3 from A --> C
move 1 from B --> A
move 2 from B --> C
move 1 from A --> C
Totally move 7 steps