Floyd–Warshall(简称Floyd算法)是一种著名的解决任意两点间的最短路径(All Paris Shortest Paths,APSP)的算法。从表面上粗看,Floyd算法是一个非常简单的三重循环,而且纯粹的Floyd算法的循环体内的语句也十分简洁。我认为,正是由于“Floyd算法是一种动态规划(Dynamic Programming)算法”的本质,才导致了Floyd算法如此精妙。因此,这里我将从Floyd算法的状态定义、动态转移方程以及滚动数组等重要方面,来简单剖析一下图论中这一重要的基于动态规划的算法——Floyd算法。
在动态规划算法中,处于首要位置、且也是核心理念之一的就是状态的定义。在这里,把d[k][i][j]定义成:
“只能使用第1号到第k号点作为中间媒介时,点i到点j之间的最短路径长度。”
图中共有n个点,标号从1开始到n。因此,在这里,k可以认为是动态规划算法在进行时的一种层次,或者称为“松弛操作”。d[1][i][j]表示只使用1号点作为中间媒介时,点i到点j之间的最短路径长度;d[2][i][j]表示使用1号点到2号点中的所有点作为中间媒介时,点i到点j之间的最短路径长度;d[n-1][i][j]表示使用1号点到(n-1)号点中的所有点作为中间媒介时,点i到点j之间的最短路径长度d[n][i][j]表示使用1号到n号点时,点i到点j之间的最短路径长度。有了状态的定义之后,就可以根据动态规划思想来构建动态转移方程。
动态转移的基本思想可以认为是建立起某一状态和之前状态的一种转移表示。按照前面的定义,d[k][i][j]是一种使用1号到k号点的状态,可以想办法把这个状态通过动态转移,规约到使用1号到(k-1)号的状态,即d[k-1][i][j]。对于d[k][i][j](即使用1号到k号点中的所有点作为中间媒介时,i和j之间的最短路径),可以分为两种情况:(1)i到j的最短路不经过k;(2)i到j的最短路经过了k。不经过点k的最短路情况下,d[k][i][j]=d[k-1][i][j]。经过点k的最短路情况下,d[k][i][j]=d[k-1][i][k]+d[k-1][k][j]。因此,综合上述两种情况,便可以得到Floyd算法的动态转移方程:
d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k]+d[k-1][k][j])(k,i,j∈[1,n])
最后,d[n][i][j]就是所要求的图中所有的两点之间的最短路径的长度。在这里,需要注意上述动态转移方程的初始(边界)条件,即d[0][i][j]=w(i, j),也就是说在不使用任何点的情况下(“松弛操作”的最初),两点之间最短路径的长度就是两点之间边的权值(若两点之间没有边,则权值为INF,且我比较偏向在Floyd算法中把图用邻接矩阵的数据结构来表示,因为便于操作)。当然,还有d[i][i]=0(i∈[1,n])。
这样我们就可以编写出最为初步的Floyd算法代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
void floyd_original() { for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) d[0][i][j] = graph[i][j]; for(int k = 1; k <= n; k++) { for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k] + d[k-1][k][j]); } } }} |
几乎所有介绍动态规划中最为著名的“0/1背包”问题的算法书籍中,都会进一步介绍利用滚动数组的技巧来进一步减少算法的空间复杂度,使得0/1背包只需要使用一维数组就可以求得最优解。而在各种资料中,最为常见的Floyd算法也都是用了二维数组来表示状态。那么,在Floyd算法中,是如何运用滚动数组的呢?
再次观察动态转移方程d[k][i][j] = min(d[k-1][i][j], d[k-1][i][k]+d[k-1][k][j]),可以发现每一个第k阶段的状态(d[k][i][j]),所依赖的都是前一阶段(即第k-1阶段)的状态(如d[k-1][i][j],d[k-1][i][k]和d[k-1][k][j])。

上图描述了在前面最初试的Floyd算法中,计算状态d[k][i][j]时,d[k-1][][]和d[k][][]这两个二维数组的情况(d[k-1][][]表示第k-1阶段时,图中两点之间最短路径长度的二维矩阵;d[k][][]表示第k阶段时,图中两点之间最短路径长度的二维矩阵)。红色带有箭头的有向线段指示了规划方向。灰色表示已经算过的数组元素,白色代表还未算过的元素。由于d[k-1][][]和d[k][][]是两个相互独立的二维数组,因此利用d[k-1][i][j],d[k-1][i][k]和d[k-1][k][j](皆处于上方的二维数组中)来计算d[k][i][j]时没有任何问题。
那如何利用一个二维数组来实现滚动数组,以减小空间复杂度呢?
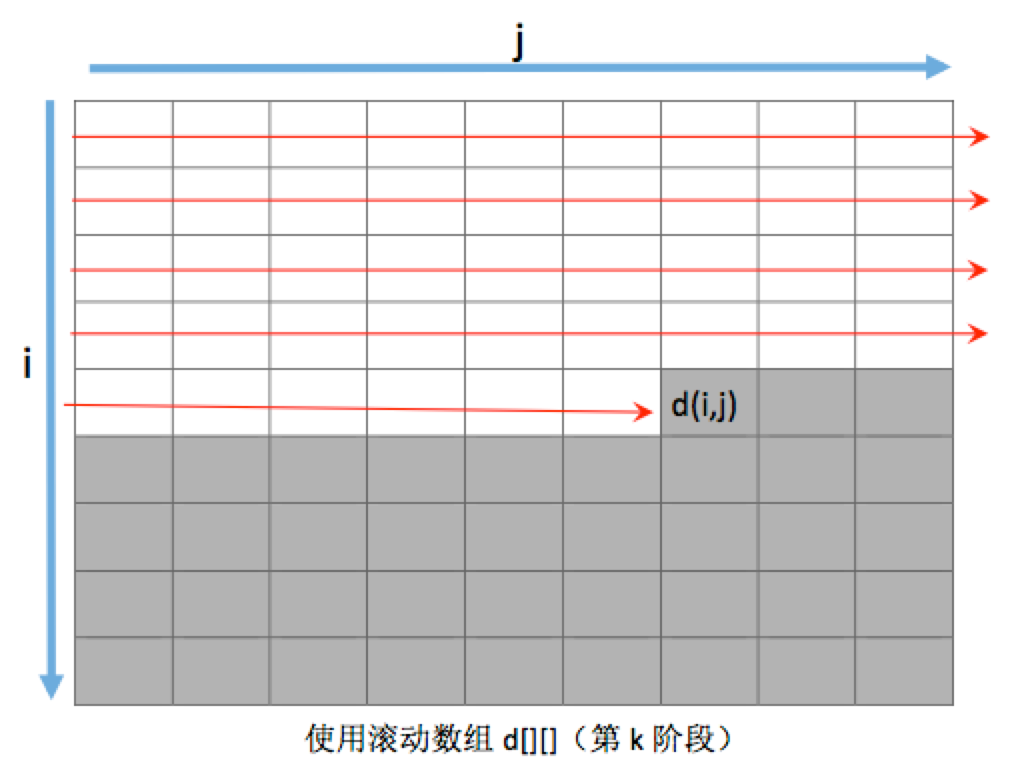
上图是使用滚动数组,在第k阶段,计算d[i][j]时的情况。此时,由于使用d[][]这个二维数组作为滚动数组,在各个阶段的计算中被重复使用,因此数组中表示阶段的那一维也被取消了。在这图中,白色的格子,代表最新被计算过的元素(即第k阶段的新值),而灰色的格子中的元素值,其实保存的还是上一阶段(即第k-1阶段)的旧值。因此,在新的d[i][j]还未被计算出来时,d[i][j]中保存的值其实就对应之前没有用滚动数组时d[k-1][i][j]的值。此时,动态转移方程在隐藏掉阶段索引后就变为:
d[i][j] = min(d[i][j], d[i][k]+d[k][j])(k,i,j∈[1,n])
赋值号左侧d[i][j]就是我们要计算的第k阶段是i和j之间的最短路径长度。在这里,需要确保赋值号右侧的d[i][j], d[i][k]和d[k][j]的值是上一阶段(k-1阶段)的值。前面已经分析过了,在新的d[i][j]算出之前,d[i][j]元素保留的值的确就是上一阶段的旧值。但至于d[i][k]和d[k][j]呢?我们无法确定这两个元素是落在白色区域(新值)还是灰色区域(旧值)。好在有这样一条重要的性质,dp[k-1][i][k]和dp[k-1][k][j]是不会在第k阶段改变大小的。也就是说,凡是和k节点相连的边,在第k阶段的值都不会变。如何简单证明呢?我们可以把j=k代入之前的d[k][i][j]=min(d[k-1][i][j], d[k-1][i][k]+d[k-1][k][j])方程中,即:
d[k][i][k]
= min(d[k-1][i][k], d[k-1][i][k]+d[k-1][k][k])
= min(d[k-1][i][k], d[k-1][i][k]+0)
= d[k-1][i][k]
也就是说在第k-1阶段和第k阶段,点i和点k之间的最短路径长度是不变的。相同可以证明,在这两个阶段中,点k和点j之间的的最短路径长度也是不变的。因此,对于使用滚动数组的转移方程d[i][j] = min(d[i][j], d[i][k]+d[k][j])来说,赋值号右侧的d[i][j], d[i][k]和d[k][j]的值都是上一阶段(k-1阶段)的值,可以放心地被用来计算第k阶段时d[i][j]的值。
利用滚动数组改写后的Floyd算法代码如下:
|
1
2
3
4
5
6
|
void floyd() { for(int k = 1; k <= n; k++) for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) d[i][j] = min(d[i][j], d[i][k] + d[k][j]);} |
因此,通过这篇文章的分析,我们可以发现,Floyd算法的的确确是一种典型的动态规划算法;理解Floyd算法,也可以帮助我们进一步理解动态规划思想。