1.原理
A:设置关键字和数组元素比较,在完成一次排序后将数组被分成两个独立的部分,其中一部分元素均比关键字小,另一部分元素均比关键字大。
B:对两部分继续进行步骤A,直至整个数组有序。
一趟快速排序的具体做法:设置两个指示变量i和j,它们的初值分别指向文件的第一个记录和最后一个记录,设关键字为pivot。首先从j向前搜索(进行j--操作),找到第一个小于pivot的aj,将它放到ai上;再从i向后搜索(进行i++操作),找到第一个大于pivot的ai,将它放到aj上,重复红字部分,直到i和j相等。
2.实例
待排序数组:[3,4,7,5,6,1,2]
第一次: 第二次: 第三次: 第四次: 第五次:
pivot=3 待排数组:[2,1] 待排数组:[5,6,7,4] 待排数组:[4,5] 待排数组:[7,6]
i=0,j=6 pivot=2 pivot=5 ...... ......
a6<pivot,令ai=2 i=0,j=1 i=3,j=6 [4,5] [6,7]
[2,4,7,5,6,1,2] a1<pivot,令ai=2 a6<pivot,令ai=4
i=1,j=6 [1,1] [4,6,7,4]
a1>pivot,令aj=4 i=1,j=1 i=4,j=6
[2,4,7,5,6,1,4] 令ai=pivot a4>pivot,令aj=6
i=1,j=5 [1,2] [4,6,7,6]
a5<pivot,令ai=1 i=4,j=5
[2,1,7,5,6,1,4] i<j时不存在aj--<pivot,
i=2,j=5 令ai=pivot
a2>pivot,令aj=7 [4,5,7,6]
[2,1,7,5,6,7,4]
i=2,j=4
i<j时不存在aj--<pivot,
令ai=pivot
[2,1,3,5,6,7,4]
注:此时第一次排序完成,
关键字左边元素均小于它,
右边均大于它
3.时间复杂度
在算法分析中,主定理(英语:master theorem)提供了用渐近符号表示许多由分治法得到的递推关系式的方法。
 ,其中
,其中
 那么
那么
 ,那么
,那么
 且对于某个常数
且对于某个常数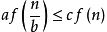 那么
那么4.代码
1 public class QuickSortTest { 2 public static void Paixu(int a[]){ //遍历数组 3 for(int i=0;i<a.length;i++){ 4 System.out.print(a[i]+" "); 5 } 6 } 7 public static void quickSort(int[] a, int low, int high) { 8 if (low < high) { 9 int i,j,pivot; 10 i = low; 11 j = high; 12 pivot = a[i]; //关键字 13 while (i < j) { 14 while(i < j && a[j] > pivot){ 15 j--; // 从右向左找第一个小于pivot的数 16 } 17 if(i < j){ 18 a[i++] = a[j]; 19 } 20 while(i < j && a[i] < pivot){ 21 i++; // 从左向右找第一个大于pivot的数 22 } 23 if(i < j){ 24 a[j--] = a[i]; 25 } 26 } 27 a[i] = pivot; 28 quickSort(a, low, i-1); 29 quickSort(a, i+1, high); 30 } 31 } 32 public static void main(String[] args) { 33 int a[] = {3,4,7,5,6,1,2}; 34 QuickSortTest.Paixu(a); 35 quickSort(a, 0, a.length-1); 36 QuickSortTest.Paixu(a); 37 38 } 39 }
