|
Apple Tree
Description There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree. The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree. The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka? 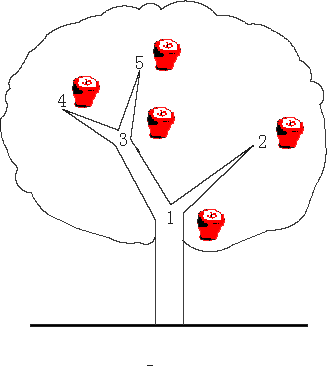 Input The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree. Output For every inquiry, output the correspond answer per line.
Sample Input 3 1 2 1 3 3 Q 1 C 2 Q 1 Sample Output 3 2 Source POJ Monthly--2007.08.05, Huang, Jinsong
|
题意:一棵具有n个节点的树,一开始,每个节点上都有一个苹果。现在给出m组动态的操作:(C,i)是摘掉第i个节点上面的苹果(若苹果不存在,则为加上一个苹果),(Q,i)是查询以第i个节点为根的子树有几个苹果(包括第i个节点)。
思路:
树状数组。这道题重点怎么建立树到树状数组的映射关系:利用dfs遍历树,对每个节点进行两次编号,第一次搜到第i个节点时的深度dep,为这个节点管辖区间的上限low[i](也为这个节点的下标),然后搜这个节点的子节点,最后搜回来后的深度dep,为这个节点管辖区间的下限high[i],如下图所示。接下来就是树状数组部分了。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=100010; struct Edge{ int to,nxt; }edge[N<<1]; int n,m,cnt,head[N],array[N]; int dep,have[N],low[N],high[N],vis[N]; //low[i]代表左顶点 , high[i]代表右顶点 void addedge(int cu,int cv){ edge[cnt].to=cv; edge[cnt].nxt=head[cu]; head[cu]=cnt++; } void DFS(int u){ low[u]=++dep; //第一次的深度,即左顶点 vis[u]=1; for(int i=head[u];i!=-1;i=edge[i].nxt){ while(!vis[edge[i].to]) DFS(edge[i].to); } high[u]=dep; //返回的深度,即右顶点 } int lowbit(int x){ return x&(-x); } void add(int rt,int val){ while(rt<=n){ array[rt]+=val; rt+=lowbit(rt); } } int sum(int rt){ int ans=0; while(rt>0){ ans+=array[rt]; rt-=lowbit(rt); } return ans; } int main(){ //freopen("input.txt","r",stdin); while(~scanf("%d",&n)){ cnt=0; memset(head,-1,sizeof(head)); dep=0; memset(have,0,sizeof(have)); memset(vis,0,sizeof(vis)); memset(array,0,sizeof(array)); for(int i=1;i<=n;i++){ have[i]=1; //1表示有苹果 add(i,1); } int u,v; for(int i=1;i<n;i++){ scanf("%d%d",&u,&v); addedge(u,v); } DFS(1); scanf("%d",&m); char op[3]; int id; while(m--){ scanf("%s%d",op,&id); if(op[0]=='Q') printf("%d\n",sum(high[id])-sum(low[id]-1)); else{ if(have[id]){ add(low[id],-1); have[id]=0; }else{ add(low[id],1); have[id]=1; } } } } return 0; }
#include<iostream> #include<cstdio> #include<cstring> using namespace std; #define L(rt) (rt<<1) #define R(rt) (rt<<1|1) const int N=100010; struct node{ int l,r; int have,sum; }tree[N<<2]; struct Edge{ int to,nxt; }edge[N<<1]; int n,m,cnt,head[N]; int dep,vis[N],low[N],high[N]; void addedge(int cu,int cv){ edge[cnt].to=cv; edge[cnt].nxt=head[cu]; head[cu]=cnt++; } void PushUp(int rt){ tree[rt].sum=tree[L(rt)].sum+tree[R(rt)].sum; } void build(int L,int R,int rt){ tree[rt].l=L; tree[rt].r=R; tree[rt].have=1; if(tree[rt].l==tree[rt].r){ tree[rt].sum=1; return ; } int mid=(L+R)>>1; build(L,mid,L(rt)); build(mid+1,R,R(rt)); PushUp(rt); } void PushDown(int rt){ tree[L(rt)].have=1; tree[L(rt)].sum=tree[L(rt)].r-tree[L(rt)].l+1; tree[R(rt)].have=1; tree[R(rt)].sum=tree[R(rt)].r-tree[R(rt)].l+1; tree[rt].have=0; } void update(int id,int rt){ if(tree[rt].l==id && tree[rt].r==id){ if(tree[rt].have==1){ tree[rt].have=0; tree[rt].sum=0; }else{ tree[rt].have=1; tree[rt].sum=1; } return ; } if(tree[rt].have) PushDown(rt); int mid=(tree[rt].l+tree[rt].r)>>1; if(id<=mid) update(id,L(rt)); else update(id,R(rt)); PushUp(rt); if(tree[L(rt)].have && tree[R(rt)].have) tree[rt].have=1; } int query(int L,int R,int rt){ if(tree[rt].l==L && tree[rt].r==R){ return tree[rt].sum; } int mid=(tree[rt].l+tree[rt].r)>>1; if(R<=mid) return query(L,R,L(rt)); else if(L>=mid+1) return query(L,R,R(rt)); else{ int a=query(L,mid,L(rt)); int b=query(mid+1,R,R(rt)); return a+b; } } void DFS(int u){ low[u]=++dep; vis[u]=1; for(int i=head[u];i!=-1;i=edge[i].nxt){ while(!vis[edge[i].to]) DFS(edge[i].to); } high[u]=dep; } int main(){ //freopen("input.txt","r",stdin); while(~scanf("%d",&n)){ cnt=0; memset(head,-1,sizeof(head)); dep=0; memset(vis,0,sizeof(vis)); int u,v; for(int i=1;i<n;i++){ scanf("%d%d",&u,&v); addedge(u,v); } DFS(1); build(1,high[1],1); char op[3]; int id; scanf("%d",&m); while(m--){ scanf("%s%d",op,&id); if(op[0]=='Q') printf("%d\n",query(low[id],high[id],1)); else update(low[id],1); } } return 0; }