原文地址:
https://www.geeksforgeeks.org/handshaking-lemma-and-interesting-tree-properties/
什么是握手引理:
握手引理是关于无向图的。在每个有限无向图中,具有奇数度的顶点数始终是偶数。握手引理是一个关于度数和的推论,有时候也直接被称之为握手引理
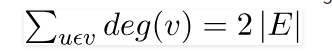
以上公式用大白话说就是:总度数=2(边数)
握手引理在数据结构中的一些具体应用:
下面是利用握手引理推理出来的一些事实:
特性一:
在一个子树数量为0或者k的k-ary树中,以下属性永远成立:
L = (k - 1)*I + 1
L:叶子节点数量
I:内部节点数量
可以分为两种情况证明:
case 1:树中只有一个节点。那么上述公式中的L为1,I为0;公式成立。
case 2:树中得节点数量大于1.
总度数 = 2(总边数)
叶子节点总度数+除根节点以外的内部节点总度数+根节点度数 = 2(总节点数量-1)
将L和I代入上述表达式
L+(I-1)*(k+1)+k = 2 * (L + I - 1)
L + k*I - k + I -1 + k = 2*L + 2I - 2
L + K*I + I - 1 = 2*L + 2*I - 2
K*I + 1 - I = L
(K-1)*I + 1 = L
得证
特性二:
在二叉树中叶子节点的数量总是比有两个孩子的节点数量多1
用公式表达就是:L = T+1
L:叶子节点数量
T:拥有两个孩子的节点
此特性基于三种情况进行分析
1,只有一个节点,那么关系为T = 0, L = 1。
2,根有两个孩子
那么根据握手引理:
除根以外具有两个孩子的节点的度+具有一个孩子的节点的度+叶子节点的度+根节点的度 = 2(节点数量-1)
L,T代入上述公式
(T-1)*3 + S*2 + L + 2 = (S + T + L - 1)*2
(T-1)*3 + L + 2 = (S + L - 1)*2
T - 1 = L - 2
T = L - 1
3,根只有一个孩子
除根以外具有一个孩子的节点的度+具有两个孩子的节点的度+叶子节点的度+根节点的度 = 2(节点数量-1)
L,T代入上式
T*3 + (S-1)*2 + L + 1 = (S + T + L - 1)*2
3*T + L -1 = 2*T + 2*L - 2
T - 1 = L - 2
T = L - 1
得证