深度学习面试题15：卷积核需要旋转180度

目录

　　举例

　　结论

　　参考资料

---

在一些书籍和博客中所讲的卷积（一个卷积核和输入的对应位置相乘，然后累加）不是真正意义上的卷积。根据离散卷积的定义，卷积核是需要旋转180的。

按照定义来说，一个输入和一个卷积核做卷积操作的流程是：

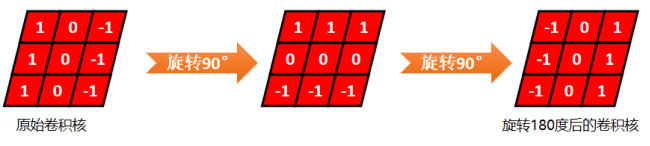
①卷积核旋转180

②对应位置相乘，然后累加

举例

下面这个图是常见的卷积运算图：

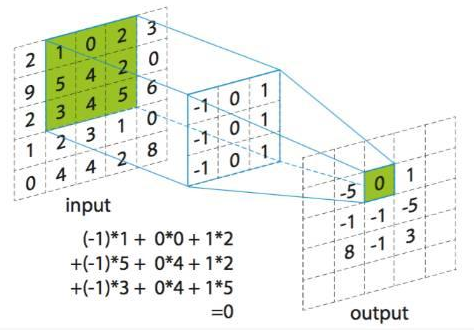
中间的卷积核，其实是已经旋转过180度的

即，做卷积的两个矩阵其实是

[[2, 1, 0, 2, 3],

 [9, 5, 2, 2, 0],

 [2, 3, 4, 5, 6],

 [1, 2, 3, 1, 0],

 [0, 4, 4, 2, 8]]

和

[[1, 0, -1],

 [1, 0, -1],

 [1, 0, -1]]

没有旋转只有乘积求和就不叫卷积运算。

但是，在tensorflow中觉得这样很纠结，所以干脆定义的卷积核直接就是旋转后的卷积核，所以tensorflow可以直接对应位置相乘，然后相加

import tensorflow as tf

# [batch, in_height, in_width, in_channels]
input = tf.constant([
    [2, 1, 0, 2, 3],
    [9, 5, 4, 2, 0],
    [2, 3, 4, 5, 6],
    [1, 2, 3, 1, 0],
    [0, 4, 4, 2, 8],
], tf.float32)
input = tf.reshape(input, [1, 5, 5, 1])

#定义旋转180后的卷积核
# [filter_height, filter_width, in_channels, out_channels]
kernel = tf.constant([
    [-1, 0, 1],
    [-1, 0, 1],
    [-1, 0, 1]
], tf.float32)
kernel = tf.reshape(kernel, [3, 3, 1, 1])

print(tf.Session().run(tf.nn.conv2d(input,kernel,[1,1,1,1],"VALID")))

[[[[-5.]   [ 0.]   [ 1.]]
  [[-1.]   [-2.]   [-5.]]
  [[ 8.]   [-1.]   [ 3.]]]]

而在scipy中，是按照严格的卷积定义来的，你定义了一个卷积核后，scipy要先将你的卷积核旋转180度，然后才对应位置相乘，再相加。 

import numpy as np
from scipy import signal

input = np.array([
    [2, 1, 0, 2, 3],
    [9, 5, 4, 2, 0],
    [2, 3, 4, 5, 6],
    [1, 2, 3, 1, 0],
    [0, 4, 4, 2, 8]
])

#定义未经旋转的卷积核
kernel = np.array([
    [1, 0, -1],
    [1, 0, -1],
    [1, 0, -1]
])
# kernel1 = np.flip(kernel1)
print(signal.convolve(input, kernel, mode="valid"))

[[-5  0  1]
 [-1 -2 -5]
 [ 8 -1  3]]

 返回目录

结论

如果你定义的是旋转180度后的卷积核，那就直接对应位置相乘再相加

如果你定义的是未经旋转的卷积核，那需要先旋转180，再对应位置相乘再相加

市面上的参考书大部分描述的卷积核都是旋转后的卷积核，我的博客中也是这样，因为这样更容易理解，不然做一次卷积，你是很难直观看出来结果的。

 返回目录

参考资料

什么！卷积要旋转180度？！

https://www.jianshu.com/p/8dfe02b61686

二维卷积的计算原理

https://wenku.baidu.com/view/f55e1bc6f90f76c661371ac5.html

 返回目录