Ⅰ.第一类斯特林数
问题描述:表示把n个人分成m组做环排列的方法数目。,求分成的(S(n,m))(方案数)。
如:1,2,3,4 和 4,1,2,3 只算一种方案。
(dp[i][j]=dp[i-1][j-1]+(i-1)*dp[i-1][j-1])
(考虑第i个物品,i可以单独构成一个非空循环排列,这样前i-1种物品构成j-1个非空循环排列,方法数为dp[i-1][j-1]);
(也可以前i-1种物品构成j个非空循环排列,而第i个物品插入之前每个物品的左边,这有(i-1)*dp[i-1][j]种方法)。
Ⅱ.第二类斯特林数
问题描述:表示把n个数分成无区别的k组,求分成的(S(n,m))(方案数)。
(dp[i][j]=dp[i-1][j-1]+dp[i-1][j]*j) (前i个数分成j组)
(当分到第i个数分为j组时,可以前i-1个数分成j-1组,自己单独一组,也就是dp[i-1][j-1])
(也可以前i-1个数已经分成了j组,然后第i个数可以分到j组的任意一组,也就是dp[i-1][j]*j)
当然,如果把n个数分成有区别的m组,方案数是(m!S(n,m)),这个自己感性理解一下。
Ⅲ.卡特兰数
(通项为f[n]=C_{2n}^n-C_{2n}^{n-1})
在证明之前抛出一个问题:现在有长2n的01序列,0和1各有n个
选0表示出栈,选1表示入栈,问有多少种合法的选择顺序(也就是在任意时刻1要大于等于0)。
(我们把0,1操作扔到一个坐标系中。1看成向右上方走一步,0看成向右下角走一步,那么最后构造完后一定走到了(2n,0))
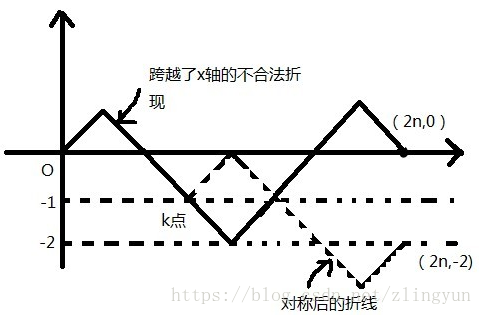
(那么非法步骤就是经过了x=-1。由于从(0,0)出发经过x=-1最后到达(2n,0),根据对对称性质等价于)
(从(0,-2)出发经过x=-1到达(2n,0),也就是在2n步中选n-1步往右下走,其余往右上走)
所以,答案是(C_{2n}^n-C_{2n}^{n-1})