Given an m x n binary grid grid where each 1 marks the home of one friend, return the minimal total travel distance.
The total travel distance is the sum of the distances between the houses of the friends and the meeting point.
The distance is calculated using Manhattan Distance, where distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|.
Example 1:
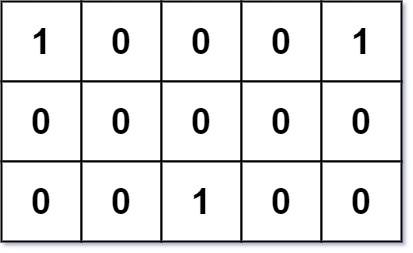
Input: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
Output: 6
Explanation: Given three friends living at (0,0), (0,4), and (2,2).
The point (0,2) is an ideal meeting point, as the total travel distance of 2 + 2 + 2 = 6 is minimal.
So return 6.
Example 2:
Input: grid = [[1,1]] Output: 1
中点距离最短,你说是就是吧。
参考:https://leetcode.com/problems/best-meeting-point/discuss/74186/14ms-java-solution
class Solution {
public int minTotalDistance(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
List<Integer> X = new ArrayList<>();
List<Integer> Y = new ArrayList<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
X.add(i);
Y.add(j);
}
}
}
return getMin(X) + getMin(Y);
}
private int getMin(List<Integer> nums) {
Collections.sort(nums);
int res = 0;
int mid = nums.get(nums.size() / 2);
for (int n : nums) {
res += Math.abs(n - mid);
}
return res;
}