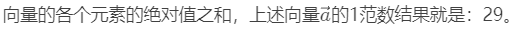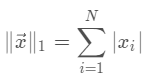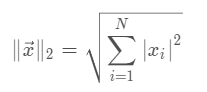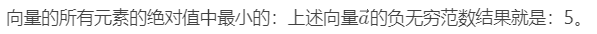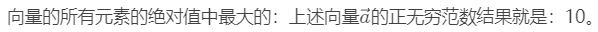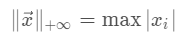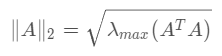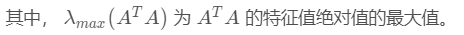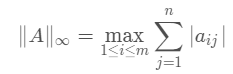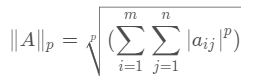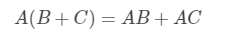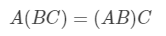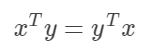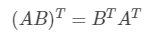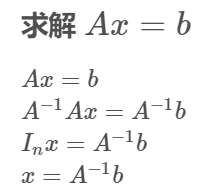标量、向量、矩阵、张量之间的联系
在深度学习中,大家肯定都知道这几个词:标量(Scalar),向量(Vector),矩阵(Matrix),张量(Tensor)。但是要是让我们具体说下他们,可能一下子找不出头绪。下面介绍一下他们之间的关系:
标量(scalar)
一个标量表示一个单独的数,它不同于线性代数中研究的其他大部分对象(通常是多个数的数组)。我们用斜体表示标量。标量通常被赋予小写的变量名称。如:a
向量(vector)
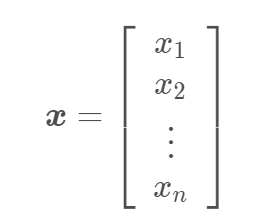
一个向量表示一组有序排列的数。通过次序中的索引,我们可以确定每个单独的数。通常我们赋予向量粗体的小写变量名称。当我们需要明确表示向量中的元素时,我们会将元素排列成一个方括号包围的纵柱:如 a.
矩阵(matrix)
矩阵是一个二维数组,其中每一个元素由两个索引所确定。一个有m行,n列,每个元素都属于 RR 的矩阵记作 A∈Rm×n. 通常使用大写变量名称,如A
张量(tensor)
超过两维的数组叫做张量。
在某些情况下,我们会讨论坐标超过两维的数组,一般的,一个数组中的元素分布在若干维坐标的规则网格中,我们称之为张量。我们使用字体 A 来表示张量“A”。张量A中坐标为(i,j,k) 的元素记作 Ai,j,k .
四者之间关系
标量是0阶张量,向量是一阶张量。
举例:
标量就是知道棍子的长度,但是你不会知道棍子指向哪儿。
向量就是不但知道棍子的长度,还知道棍子指向前面还是后面。
张量就是不但知道棍子的长度,也知道棍子指向前面还是后面,还能知道这棍子又向上/下和左/右偏转了多少。
向量和矩阵的范数归纳
向量的范数(norm)

向量的1范数:
向量的2范数:
向量的负无穷范数:
向量的正无穷范数:
向量的p范数:
矩阵的范数

当向量取不同范数时, 相应得到了不同的矩阵范数。
矩阵的1范数(列范数):
矩阵的每一列上的元素绝对值先求和,再从中取个最大的,(列和最大);
矩阵的2范数:
矩阵的无穷范数(行范数):
矩阵的每一行上的元素绝对值先求和,再从中取个最大的,(行和最大).
上述矩阵A的行范数先得到[6;16] ,再取最大的最终结果就是:16。
矩阵的核范数:
矩阵的奇异值(将矩阵svd分解)之和,这个范数可以用来低秩表示(因为最小化核范数,相当于最小化矩阵的秩——低秩)
矩阵的L0范数:
矩阵的非0元素的个数,通常用它来表示稀疏,L0范数越小0元素越多,也就越稀疏.
上述矩阵A 最终结果就是:6
矩阵的L1范数:
矩阵中的每个元素绝对值之和,它是L0范数的最优凸近似,因此它也可以表示稀疏.
上述矩阵AAA最终结果就是:22。
矩阵的F范数:
矩阵的各个元素平方之和再开平方根,它通常也叫做矩阵的L2范数,它的有点在它是一个凸函数,可以求导求解,易于计算.
上述矩阵A最终结果就是:10.0995。
矩阵的 p范数:
其他线性代数的标量学习
行列式:(数学上定义为一个函数)
转置(transpose)

注意:
向量可以看作只有一列的矩阵, 对应地,向量的转置结果可以看作只有一行的矩阵。
标量的转置等于自身。
矩阵运算
矩阵可以进行加法、乘法计算。
矩阵乘法(Matrix Product)
两个矩阵的标准乘积不是两个矩阵中对应元素的乘积。
向量的点积(dot Product):(可以理解成矩阵乘积Matrix Product)
注意:
向量点积结果必然是一个实数,即一个一行一列的矩阵。
矩阵乘法分配律
矩阵乘积结合律
注意:矩阵乘积并不满足交换律,然而,两个向量的点积满足交换律
矩阵乘积的转置有着简单的形式
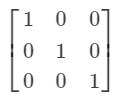
单位矩阵(identity matrix)
单位矩阵所有沿对角线的元素都是1, 而其它位置的所有元素都是0。
任意向量和单位矩阵相乘,都不会改变。
逆矩阵
endl;