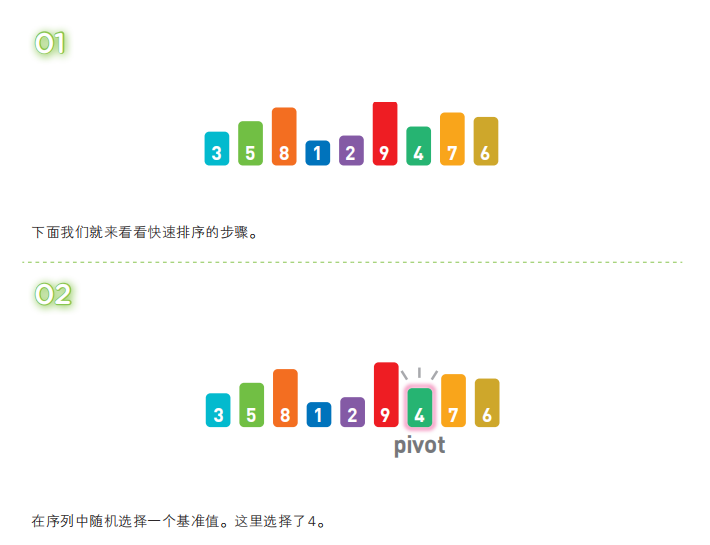
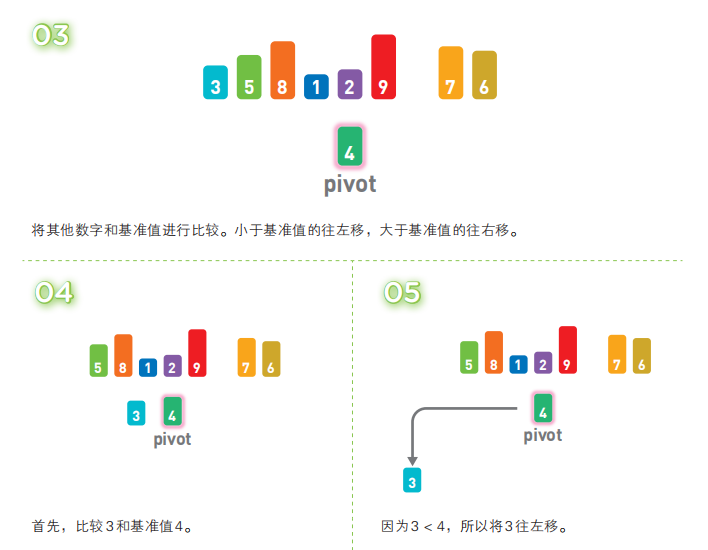
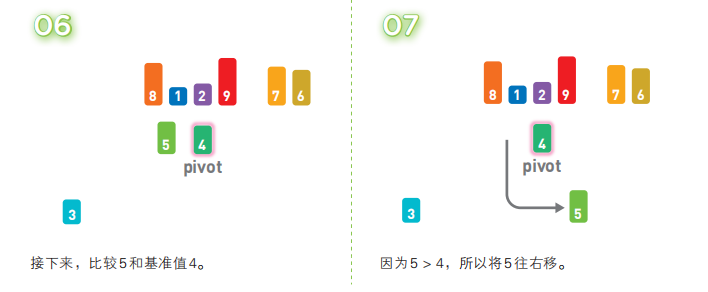
快速排序算法首先会在序列中随机选择一个基准值(pivot),然后将除了基准值以外的数分为“比基准值小的数”和“比基准值大的数”这两个类别,再将其排列成以下形式。
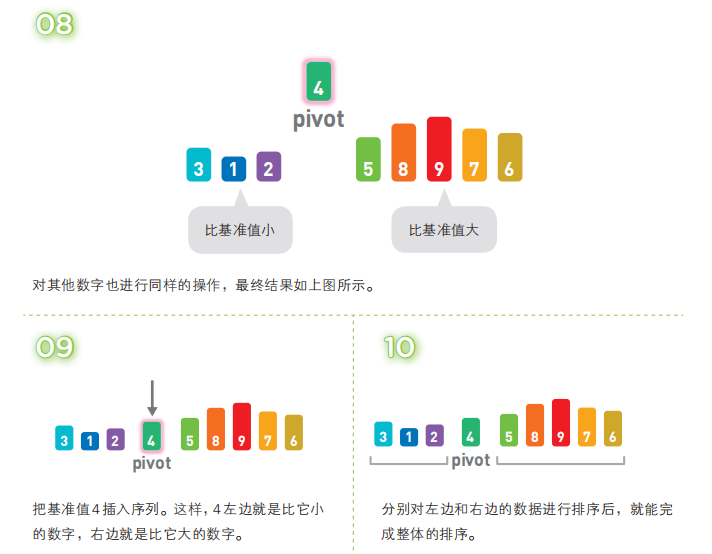
[ 比基准值小的数 ] 基准值 [ 比基准值大的数 ]
接着,对两个“[ ]”中的数据进行排序之后,整体的排序便完成了。对“[ ]”里面的数据进行排序时同样也会使用快速排序。

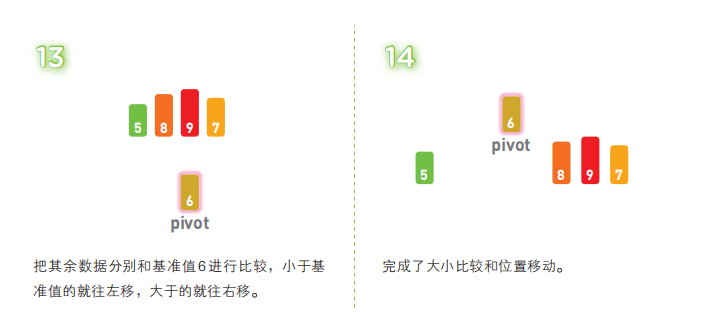
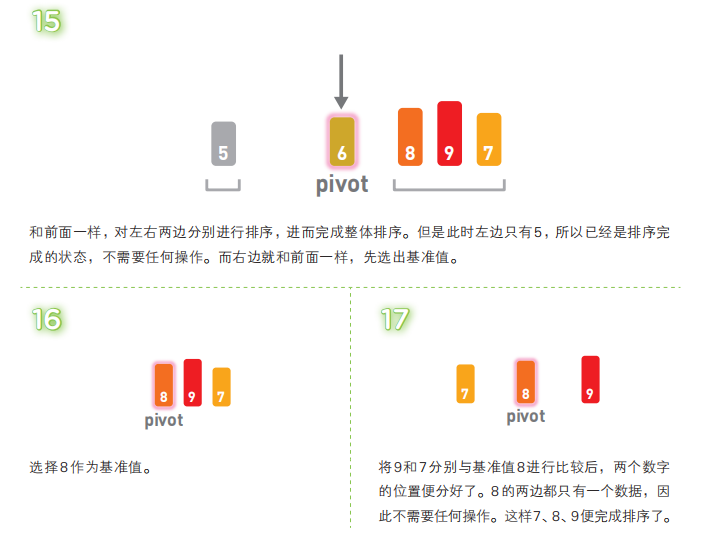
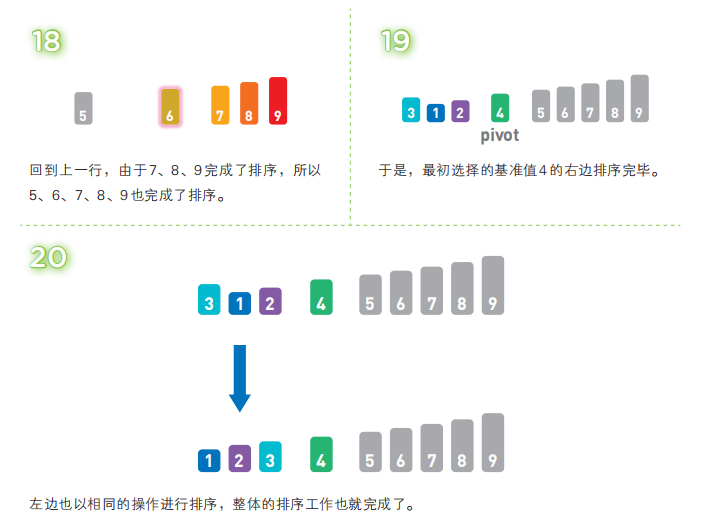
解说
分割子序列时需要选择基准值,如果每次选择的基准值都能使得两个子序列的长度为原本的一半,那么快速排序的运行时间和归并排序的一样,都为 O(nlogn)。和归并排序类似,将序列对半分割 log2n 次之后,子序列里便只剩下一个数据,这时子序列的排序也就完成了。因此,如果像下图这样一行行地展现根据基准值分割序列的过程,那么总共会有 log2n 行。
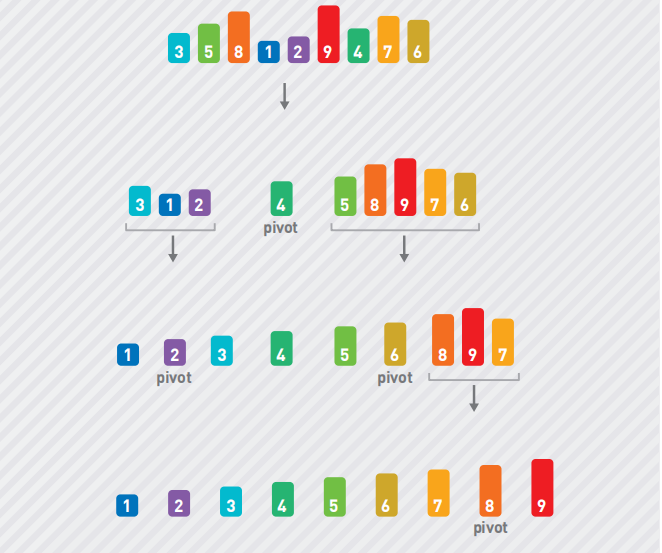
每行中每个数字都需要和基准值比较大小,因此每行所需的运行时间为 O(n)。由此可知,整体的时间复杂度为 O(nlogn)。如果运气不好,每次都选择最小值作为基准值,那么每次都需要把其他数据移到基准值的右边,递归执行 n 行,运行时间也就成了 O(n2)。这就相当于每次都选出最小值并把它移到了最左边,这个操作也就和选择排序一样了。此外,如果数据中的每个数字被选为基准值的概率都相等,那么需要的平均运行时间为 O(nlogn)。
补充说明
快速排序是一种“分治法”。它将原本的问题分成两个子问题(比基准值小的数和比基准值大的数),然后再分别解决这两个问题。子问题,也就是子序列完成排序后,再像一开始说明的那样,把他们合并成一个序列,那么对原始序列的排序也就完成了。不过,解决子问题的时候会再次使用快速排序,甚至在这个快速排序里仍然要使用快速排序。只有在子问题里只剩一个数字的时候,排序才算完成。像这样,在算法内部继续使用该算法的现象被称为“递归”。实际上前一节中讲到的归并排序也可看作是一种递归的分治法。