2018-07-14 09:57:59
问题描述:

问题求解:
本题本质上是个挺模板的题目。本质是一个求最后每个落点的数目,用总的数目来除有所可能生成的可能性。这种计数的问题可以使用动态规划来进行解决。
在本题中有两个注意点:
1)可以使用两个数组滚动使用来实现重复利用,这里我的实现使用了一个trick就是结合奇偶性来完成数组滚动;
2)dp数组需要定义成double类型的,如果定义成int类型的,在后期会出现溢出的问题。
public double knightProbability(int N, int K, int r, int c) {
double[][][] dp = new double[2][N][N];
int[][] dir = new int[][]{
{-1, -2},
{-2, -1},
{1, -2},
{2, -1},
{-1, 2},
{-2, 1},
{1, 2},
{2, 1},
};
dp[0][r][c] = 1;
for (int k = 0; k < K; k++) {
fill2D(dp, (k + 1) & 1, N);
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
for (int m = 0; m < 8; m++) {
int u = i + dir[m][0];
int v = j + dir[m][1];
if (u < 0 || u >= N || v < 0 || v >= N) continue;
dp[(k + 1) & 1][u][v] += dp[k & 1][i][j];
}
}
}
}
double total = 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
total += dp[K & 1][i][j];
}
}
return total / Math.pow(8, K);
}
private void fill2D(double[][][] array, int layer, int n) {
for (int i = 0; i < n; i++) Arrays.fill(array[layer][i], 0);
}
Follow up:
问题描述:
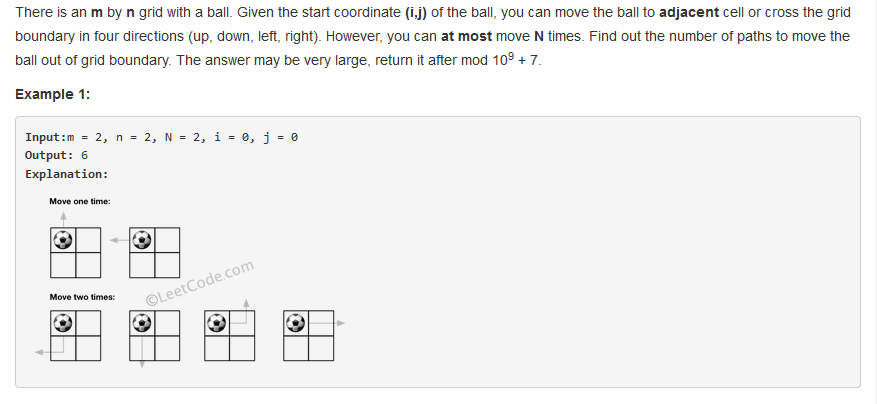
问题求解:
如出一辙。
public int findPaths(int m, int n, int N, int i, int j) {
int[][] dp = new int[m][n];
dp[i][j] = 1;
int res = 0;
int mod = (int)Math.pow(10, 9) + 7;
int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
for (int step = 0; step < N; step++) {
int[][] cur = new int[m][n];
for (int pi = 0; pi < m; pi++) {
for (int pj = 0; pj < n; pj++) {
for (int[] dir : dirs) {
int x = pi + dir[0];
int y = pj + dir[1];
if (x < 0 || x >= m || y < 0 || y >= n) {
res = (res + dp[pi][pj]) % mod;
}
else cur[x][y] = (cur[x][y] + dp[pi][pj]) % mod;
}
}
}
dp = cur;
}
return res;
}