摘要: C语言的基本数据类型,大家从学生时代就开始学习了,但是又有多少人会试图从底层的角度去学习呢?这篇文章会用一问一答的形式,慢慢解析相关的内容和困惑。
本文分享自华为云社区《从深入理解底层的角度学习C语言之基本数据类型》,作者: breakDawn 。
C语言的基本数据类型,大家从学生时代就开始学习了,但是又有多少人会试图从底层的角度去学习呢?这篇文章会用一问一答的形式,慢慢解析相关的内容和困惑。
- 数据类型位数和符号
- 数据类型转换
- 浮点数
数据类型位数和符号
Q: C里的signed 和unsigned类型的区别是什么?
A:拿unsigned char无符号char 和 signed char有符号char举例(因为他们都是1字节,比较好举例子)
假设某个局部变量a,内存里存的都是0xff(即二进制11111111)
执行printf("%d",a)时, 输出的是255,还是-1呢?
如果a是无符号,那就是255。
如果a是有符号,那就是-1。
Q:为什么有符号的0xff输出的是-1?
A:这个就是补码的概念。
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
- 补码的计算方式:如果是-1,则负号就是首位的“1”, 而“-1”里的1作为二进制是0000001,取反+1,得到1111111, 和首位1拼接,变成了11111111.
- 进行printf打印时,C语言通过变量类型,确认11111111的首位是符号位,于是通过补码的反向计算,得到实际真值为-1。
- 如果是无符号,则C语言通过变量类型,确认11111111的首位不是符号位,不需要反向计算,于是直接输出255。
原码、反码、补码对于+1和-1的表示如下
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
Q: 已知正负数默认都是补码的形式,为什么不能用原码表示数字呢?即只用第一个标识符号位,后面7位就是代表真实绝对值
A:计算机CPU做计算时,无法区别符号位,只会死板的将8位数字进行加法计算。
假设做减法,就和下面那样
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
可以看到符号位的信息会误导减法的计算。
Q: 那为什么不用能反码呢
A:因为反码对于0的表示有两种情况,11111111可以代表-0,而00000000代表+0,相当于浪费了。
而补码不存在这个情况。11111111代表-1,00000000代表0。
Q: 为什么要有补码?补码有什么好处?
A:当计算机执行1 - 1时, 希望都是用加法的动作来做,且不希望做if-else判断,根据符号位去判断正负再做加减,对计算机的消耗是很大的。
使用补码的机制,则可以将1-1转成变成1+(-1)
那么-1就是补码0xff,和0x01相加,变成了0,即不需要做真正的减法即可
Q: 刚才提到CPU希望都是位加法,不肯做减法,为什么?
A:因为CPU的减、乘、除都是基于加法、移位等操作实现的。
加法过程依赖CPU的ALU累加器,累加器背后的电路是数字电路异或门和与门的组合。
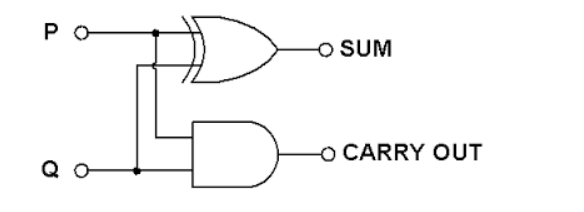
Q: 为什么补码表示的情况下,范围是-128到127?为什么补码会比原码和反码多一位?
A:就是上面提到的0的问题。原码的10000000、00000000都表示0,补码的11111111和00000000都表示0,而补码只有1个0的表示
同时补码有一个100000000, 把后7位取反+1,等同于-128。
原码、反码、补码知识详细讲解(此作者是我找到的讲的最细最明白的一个)
Q: 计算机在CPU做计算时,怎么识别是无符号还是有符号?
A:CPU 所处理的寄存器、内存中的数本身无符号信息。CPU 做加减法时会一起做无符号数的进位/有符号数的溢出标志,并不专门对待有符号数和无符号数。
有无符号的区别是只属于(中)高级语言的概念,反映到机器语言上,是跟运算及与其结果相关的指令上的区别,而不会反映到 CPU 所处理的数本身。
即CPU处理时,统一用加法处理,但是否要做求补等操作,取决于提供的运算指令。
Q: C语言的char是signed char还是unsigned char?
A: 当你定义为char时, 可能是signed char,也可能是unsigned char。
这个取决于你编译器的实现。
-funsigned-char : 设置为 unsigned char
-fno-signed-char : 设置为 非 signed char
-fsigned-char : 设置为 signed char
-fno-unsigned-char : 设置为 非 unsigned char
Q: int有可能像char一样,即可能是signed int也可能是unsigned int吗?
A:int一定是有符号int。不会因为编译器不同而不同。
Q: 为什么char可以区分有符号或者无符号,但是int只能默认为signed int ?
A:个人理解和应用场景有关,char不一定会参与计算,而int大部分情况下都是有符号计算,因此默认为signed int比较好。
Q: ILP32、LP64、LLP64分别是什么?
A:指的是这个操作系统中,有哪些类型分别是多少位的意思。
I指int
L指long
LL指long long
P指point指针
32和64就是分别指32位和64位。
- 32位系统一定是ILP32模型
- 64位系统中,unix一般是LP64,而windows则是LLP64
即linux中,long是64位, 而在windows中,long是32位,而只有long long是64位
Q: 为什么windos要用LLP64这么奇怪的模型?这个模型里, long是32位,long long 才是64位。
A:来自知乎陈硕大佬的回答:
我猜,是因为 Windows API 从 16-bit 升级到 32-bit 发生得太晚了——大约是随 1995 年发布的 Windows 95 而普及 。
虽然之前有 Windows NT 3.x 和 Win32s,但似乎比较小众。
而 Unix 从 16-bit 升级到 32-bit 发生在 1980 年前后,当时运行在 VAX 上的 Unix/32V 和 3BSD 都是 32-bit 的。
造成的结果是,两边的程序对 short/int/long 的长度形成了不同的习惯认知:
Unix 程序习惯了 int 是 32-bit,而 long 不一定只有 32-bit。Windows/DOS 习惯了 long 是 32-bit,而 int 有可能是 16-bit 或 32-bit,因为刚刚从 16-bit 升级上来嘛。
当往 64-bit 升级的时候,如果把 Windows 的 long 升级到 64-bit,会破坏原来很多程序的假设,只好用个新的类型来表示 64-bit 整数了。反正 LONGLONG 在 32-bit 程序中也是 64-bit 整数,干脆用它好了。
详细的数据类型展示:
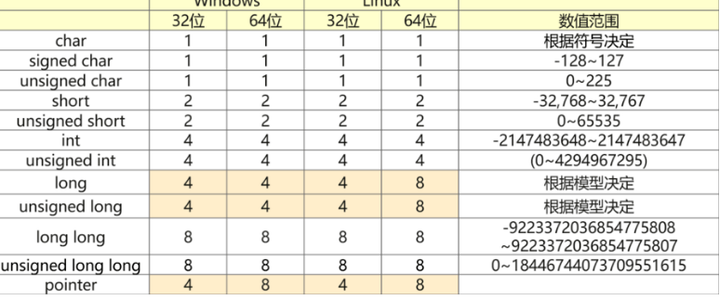
PS: 从上面可以看到java虚拟机的一个优势,就是对开发者而言,屏蔽了各不同系统情况下的数据位数。
Q: 那么又有个问题,java虚拟机如何实现不同平台可以跑相同的java代码,不用担心底层数据类型的?
A:如图所示,class字节码都是同一份,但是不同的系统,会有不同的虚拟机解释器实现,在解释器实现里处理了不同的数据类型位数情况。
数据类型转换
Q: C里的隐式类型转换有什么规律?
A:
- 占用字节数少的类型,向占用字节数多的类型转换;
int->long - 占用字节数相同情况下,有符号向无符号转换;
int->unsigned int - 整数类型向浮点类型转换;
int -> double - 单精度向双精度转换;
float->double
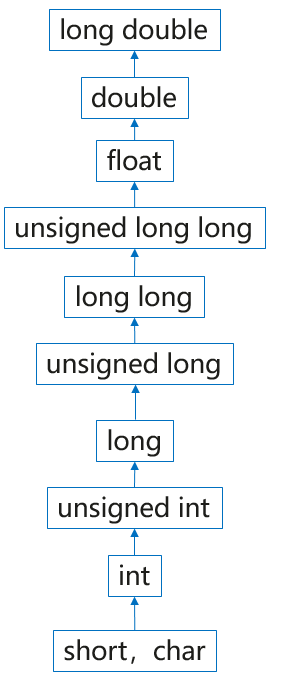
Q: 下面这个例子输出多少,为什么?
A:
void Test() { int a = -1; unsigned b = 10; if (a > b) { printf("a is greater than b.\n"); } else { printf("a is less than or equal b.\n"); } }
输出a>b即a is greater than
因为a=-1,存储的二进制是11111111, 强转成unsigned时,二进制没有变,但是对编译器而言表示的大小变成了255了。
浮点数
float、double、long double的比特数、有效位数、数值范围如下:
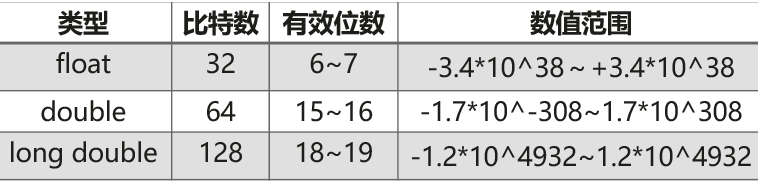
Q: 下面这个代码输出什么?
#include <stdio.h> int main(void) { float a = 9.87654321; float b = 9.87654322; if(a > b) { printf("a > b\n"); } else if(a == b) { printf("a == b\n"); } else { printf("a < b\n"); } return 0; }
A:输出"a=b", 因为float最多7位有效小数点位数。
Q: 32位float,1bit为符号位,23bit为位数,8bit为指数, 这3个划分是如何得到float的有效位数以及数值范围的?
A:IEEE754标准理解。
有人问为什么要学习这个?
对于高精度场景下的浮点计算,掌握IEEE754的标准很重要,否则无法理解高精度场景时计算过程出现的各种问题, 特别是一些金融场景,对于小数点后面的数字会特别敏感。
Q:java的BigDecimal类可以表示任意精度,原理是啥?
A:BigDecimal的原理很简单,就是将小数扩大N倍,转成整数后再进行计算,同时结合指数,得出没有精度损失的结果。
以long型的intCompact和scale来存储精确的值。