adaboost 基于错误提升分类器

引自（机器学习实战）

简单概念

Adaboost是一种弱学习算法到强学习算法，这里的弱和强学习算法，指的当然都是分类器，首先我们需要简单介绍几个概念。

1：弱学习器：在二分情况下弱分类器的错误率会低于50%。其实任意的分类器都可以做为弱分类器，比如之前介绍的KNN、决策树、Naïve Bayes、logiostic回归和SVM都可以。这里我们采用的弱分类器是单层决策树，它是一个单节点的决策树。它是adaboost中最流行的弱分类器，当然并非唯一可用的弱分类器。即从特征中选择一个特征来进行分类，该特征能使错误率达到最低，注意这里的错误率是加权错误率，为错分样本(1)与该样本的权重的乘积之和(不明白看后面代码)。

更为严格点的定义：

 

强学习：一个概念如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么，这个概念是强可学习的；

弱学习：一个概念如果存在一个多项式的学习算法能够学习它，并且学习的正确率仅比随机猜测略好(高于50%)，那么，这个概念是弱可学习的；

强可学习与弱可学习是等价的。并且理论证明可以将若干个弱学习分类器通过线性叠加提升为强学习分类器。

 

2：强学习器：识别准确率很高并能在多项式时间内完成的学习算法

3：集成方法：就是将不同的分类器组合在一起，这种组合的结果就是集成方法或者称为元算法。它可以是不同算法的集成，也可以是同一算法在不同设置下的集成，还可以是数据集的不同部分分配给不同分类器后的集成。

4：通常的集成方法有bagging方法和boosting方法，adaboost是boosting的代表算法，他们的区别在于：bagging方法(bootstrapaggregating)，中文为自举汇聚法，是从原始数据集重选择(有放回，可以重复)得到S个新数据集的一种技术，每个新数据集样本数目与原数据集样本数目相等，这样就可以得到S个分类器，再对这S个分类器进行叠加，他们的权重都相等(当然这里S个分类器采用的分类算法不一样的话，可以考虑使用投票)，这样就可以得到一个强学习器。

而boosting方法是通过集中关注被已有分类器错分的那些数据来获得新的分类器，boosting算法中分类的权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度。这里不是太明白的话，看完后面adaboost算法就会明白这句话的含义。

5：adaboost算法：机器学习实战这本书上的描述和论文中的描述是一致的，见下面(前两幅是书中描述，后一副是论文中描述)。

 

adaboost运行过程如下：训练数据中的每一个样本，赋予其一个权重，这些权重构成了向量D，一开始，这些权重都初始化成相等值。

首先在训练数据中训练出一个弱分类器并计算改分类器的错误率，然后在同一数据集上再次训练弱分类器。在分类器的第二次训练当中

，将会重新调整每个样本的权重，其中第一次分对的样本的权重将会降低，而第一次分错的样本权重将会提高。为了从所有弱分类器中

得到最终的分类结果，adaboost为每个分类器都分配一个权重值alpha,这些alpha值都是基于每个弱分类器的错误率进行计算的。

其中错误率定义为

　　　　　　　　　　　　

alpha计算公式

　　　　　　　　　　　　　　

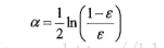
问题：上题中的alpha为什么是这个公式呢？解释为：-----再看没看懂！！

 

 （1）基于单层决策树构建弱分类器

def loadSimDat():  
    dataMat = matrix([[1, 2.1],  
                      [2.0, 1.1],  
                      [1.3, 1.0],  
                      [1.0, 1.0],  
                      [2.0, 1.0]])  
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]  
    return dataMat, classLabels  
  
# 单层决策树生成函数  
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data  
    retArray = ones((shape(dataMatrix)[0],1))  
    if threshIneq == 'lt':  
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0  
    else:  
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0  
    return retArray  
  
  
def buildStump(dataArr, classLabels, D):  
    dataMatrix = mat(dataArr); labelMat = mat(classLabels).T  
    m,n = shape(dataMatrix)  
    numSteps = 10.0; bestStump = {}; bestClassEst = mat(zeros((m,1)))  
    minError = inf  
    for i in range(n):  
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();  
        stepSize = (rangeMax - rangeMin)/numSteps  
        for j in range(-1, int(numSteps)+1):  
            for inequal in ['lt','gt']:  
                threshVal = (rangeMin + float(j)*stepSize)  
                predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal)  
                errArr = mat(ones((m,1)))  
                errArr[predictedVals == labelMat] = 0  
                weightedError = D.T * errArr           #这里的error是错误向量errArr和权重向量D的相应元素相乘得到的即加权错误率  
                #print "split: dim %d, thresh %.2f, thresh inequal: %s, the weighted error is %.3f" %(i, threshVal, inequal, weightedError)  
                if weightedError < minError:  
                    minError = weightedError  
                    bestClassEst = predictedVals.copy()  
                    bestStump['dim'] = i  
                    bestStump['thresh'] = threshVal  
                    bestStump['ineq'] = inequal  
    return bestStump, minError, bestClassEst  

注意这里有三层循环构建了单层决策树，最外层循环为遍历特征，次外层循环为遍历的步长，最内层为是否大于或小于阀值。构建的最小错误率为加权错误率，这就是为什么增加分错样本的权重，因为分错样本的权重增加了，下次如果继续分错，加权错误率会很大，这就不满足算法最小化加权错误率了。此外，加权错误率在每次迭代过程中一定是逐次降低的。。

 （2）完整的adaboost算法

def adaBoostTrainDS(dataArr, classLabels, numIt = 40):  
    weakClassArr = []  
    m = shape(dataArr)[0]  
    D = mat(ones((m,1))/m)  
    aggClassEst = mat(zeros((m,1)))  
    for i in range(numIt):  
        bestStump, error, classEst = buildStump(dataArr, classLabels, D)  
       # print "D:", D.T  
        alpha = float(0.5 * log((1.0 - error)/max(error, 1e-16)))   #确保在没有错误时不会发生除零溢出  
        bestStump['alpha'] = alpha  
        weakClassArr.append(bestStump)  
        #print "classEst:", classEst.T  
        expon = multiply(-1 * alpha * mat(classLabels).T, classEst)    #乘法用于区分是否正确或者错误样本  
        D = multiply(D, exp(expon))  
        D = D/D.sum()            # 归一化用的  
        aggClassEst += alpha * classEst    #累加变成强分类器  
        aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T, ones((m,1)))  
        errorRate = aggErrors.sum()/m  
        print "total error: ", errorRate, "
"  
        if errorRate == 0.0: break  
    return weakClassArr, aggClassEst  

注意代码中的一个技巧max(error,le-16)用于确保在没有错误时不会发生除零溢出。

(3)   测试算法：基于adaboost的分类

#adaboost分类函数  
def adaClassify(datToClass, classifierArr):  
    dataMatrix = mat(datToClass)  
    m = shape(dataMatrix)[0]  
    aggClassEst = mat(zeros((m,1)))  
    for i in range(len(classifierArr)):  
        classEst = stumpClassify(dataMatrix, classifierArr[i]['dim'], classifierArr[i]['thresh'], classifierArr[i]['ineq'])  
        aggClassEst += classifierArr[i]['alpha']*classEst  
        print aggClassEst  
    return sign(aggClassEst)  

此外如何理论上证明弱学习分类器可以通过线性叠加提升为强学习分类器，有两种证明方法：(1)通过误差上界，(2)通过adaboost的损失函数（指数损失函数）来证明。推导看以参看：http://blog.csdn.net/v_july_v/article/details/40718799， 其中我只看了误差上界的推导。

误差上界的结论表明，AdaBoost的训练误差是以指数速率下降的。另外，AdaBoost算法不需要事先知道下界γ，AdaBoost具有自适应性，它能适应弱分类器各自的训练误差率 。

只要保证弱分类器的错误率小于0.5，每次e^(2Mr^2))肯定是不断减小的