UVa 11346

链接：

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2321

题意：

在[-a,a]*[-b,b]区域内随机取一个点P，求以(0,0)和P为对角线的长方形面积大于S的概率（a,b>0，S≥0）。
例如a=10，b=5，S=20，答案为23.35％。

分析：

根据对称性，只需要考虑[0,a]*[0,b]区域取点即可。面积大于S，即xy>S。xy=S是一条双曲线，
所求概率就是[0,a]*[0,b]中处于双曲线上面的部分。
为了方便，还是求曲线下面的面积，然后用总面积来减，如图所示。

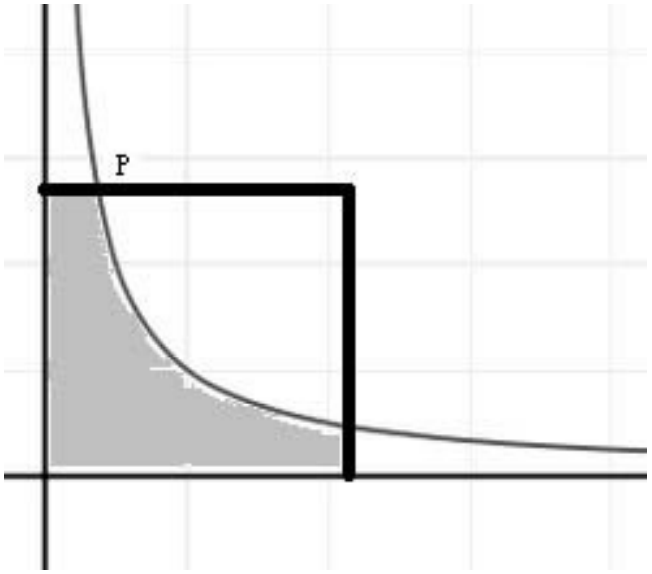
设双曲线和区域[0,a]*[0,b]左边的交点P是(S/b, b)，因此积分就是：

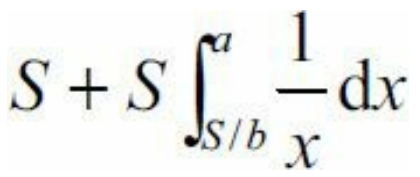
查得1/S的原函数是ln(S)，因此积分部分就是ln(a)-ln(S/b) = ln(ab/S)。
设面积为m，则答案为(m - s - s *ln(m/s)) / m。
注意这样做有个前提，就是双曲线和所求区域相交。如果s>ab，则概率应为0；
而如果s太接近0，概率应直接返回1，否则计算ln(m/s)时可能会出错。

代码：

import java.io.*;
import java.util.*;
import static java.lang.Math.*;

public class Main {
    Scanner cin = new Scanner(new BufferedInputStream(System.in));
    
    void MAIN() {
        int T = cin.nextInt();
        while(T --> 0) {
            double a = cin.nextDouble();
            double b = cin.nextDouble();
            double s = cin.nextDouble();
            double ans, m = a * b;
            if(s > m) ans = 0;
            else if(s < 1e-6) ans = 1;
            else ans = (m - s - s*log(m/s)) / m;
            System.out.printf("%.6f%%
", ans * 100);
        }
    }
    
    public static void main(String args[]) { new Main().MAIN(); }
}