Q1代价函数
(1)假设神经网络的训练样本有m个,每一个包含一组输入x和一组输出信号y,L表示神经网络的层数,Sl表示每一层的神经元个数,SL代表最后一层中处理单元的个数。
则代价函数为(同样不对θ0正则化):
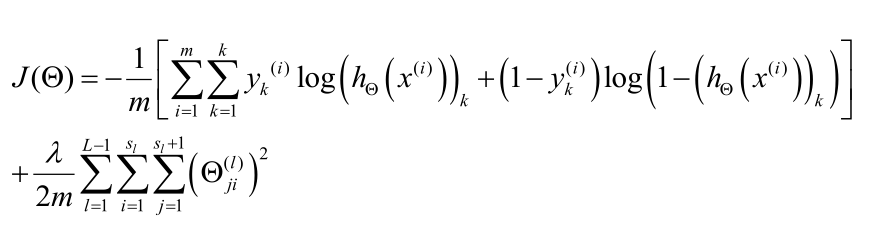
Q2反向传播算法
误差计算公式,注意第一列作为输入是没有误差的。
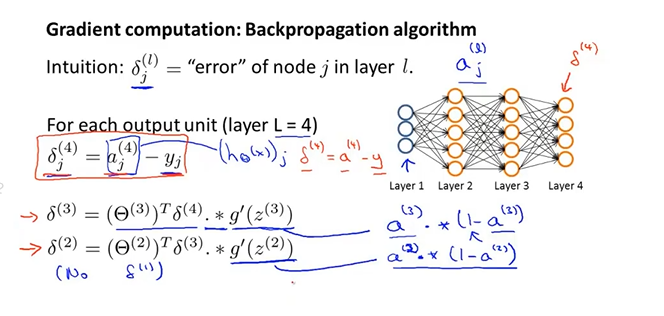
前向传播算法:
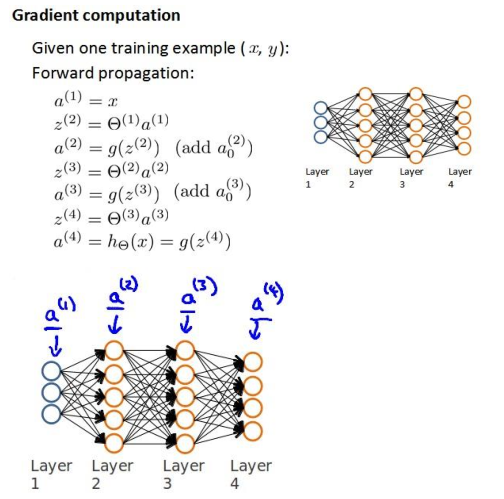
用δ表示误差,则δ(4)=a(4)-y
前一层的误差为:
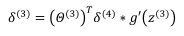
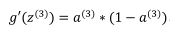
再前一层的误差为:
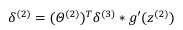 。
。
输入层不存在误差。
每一层有了误差之后,即可分别进行求偏导,然后更新θ。

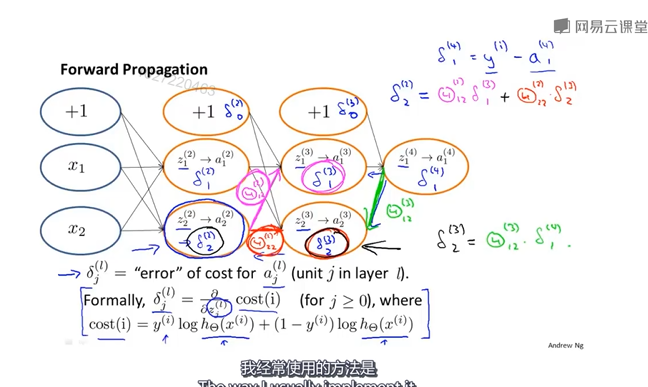
Q3反向传播算法的直观理解
误差值的计算则是从后向前计算,并且偏置误差可以不算,作为常数,对于求导没有影响。
Q4实现注意:展开参数
参数不再是向量而是矩阵
Q5梯度检验
http://dy.163.com/v2/article/detail/DHCUPPTC0511FERQ.html
用某点领域的两个点的连线的斜率作为该点的估算值,然后用该值与神经网络计算出来的值作比较。

Q6随机初始化
参数的初始化应该随机的,如果是相同的值的话,第二层的所有激活单元都会有相同的值,后面也类似。
Q7综合起来
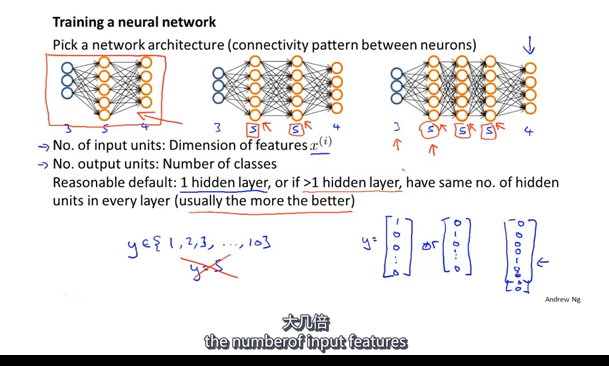
使用神经网络时的步骤:
(1)网络结构:第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少单元。
第一层的单元数即为我们训练集的特征数量。
最后一层的单元数是我们训练集的结果的类的数量。
(2)训练神经网络:
1.参数的随机初始化;(一般很小接近于0)
2.利用正向传播方法计算所有的hθ(x);
3.编写计算代价函数J的代码;
4.利用反向传播方法计算所有的偏导数;
5.利用数值检验方法得到的偏导数取检验这些偏导数,如果差别很小,则说明神经网络合理性;
6.使用优化算法(梯度下降)来最小化代价函数(反向传播算法可以计算出下降的方向,梯度下降算法则沿着该方向进行下降)。