【洛谷P2598】狼和羊的故事【网络流】

题目大意：

题目链接：https://www.luogu.org/problemnew/show/P2598
$n imes m$的网格中有些格子上有狼，有些有羊，有些是空地。网格外边已经有一层栅栏，求至少还需要多少栅栏才可以把狼和羊分开。

---

思路:

很明显是一道网络流最小割的题目。众所周知，最小割=最大流。
源点连向所有含有羊的格子，流量为$Inf$，所有含有狼的格子连向汇点，流量为$Inf$。
接下来，每个相邻且不是同一种动物的点连边，流量为$1$。很明显流了的边就相当于建立栅栏，而且满足栅栏长度最小。两只狼、两只羊相连并没有任何意义。这样可以减少复杂度。

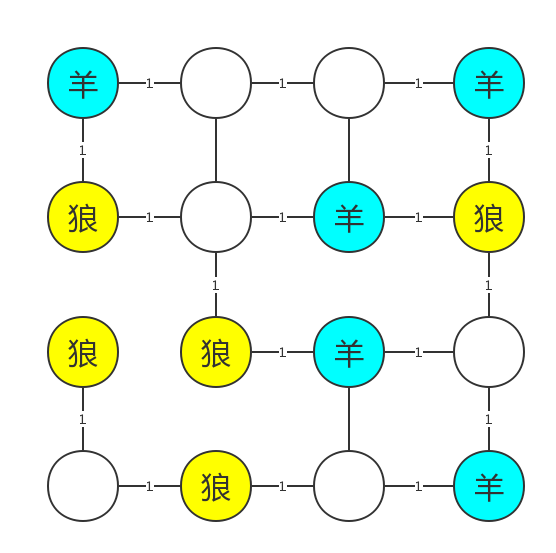
加上当前弧优化即可过掉本题。

---

代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int N=200010;
const int M=510;
const int di[]={0,0,0,-1,1};
const int dj[]={0,1,-1,0,0};
int n,m,a[M][M],S,T,tot=1,cur[N],head[N],dep[N],maxflow,sum,x,y;

struct edge
{
    int next,flow,to;
}e[N*2];

void add(int from,int to,int flow)
{
    tot++;
    e[tot].flow=flow;
    e[tot].to=to;
    e[tot].next=head[from];
    head[from]=tot;
}

bool bfs()  //分层
{
    memset(dep,0x3f3f3f3f,sizeof(dep));
    memcpy(cur,head,sizeof(cur));
    queue<int> q;
    dep[S]=1;
    q.push(S);
    while (q.size())
    {
        int u=q.front();
        q.pop();
        for (int i=head[u];~i;i=e[i].next)
        {
            int v=e[i].to;
            if (dep[v]>dep[u]+1&&e[i].flow)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    return dep[T]<1e9;
}

int dfs(int u,int flow)
{
    int low=0;
    if (u==T)
    {
        maxflow+=flow;
        return flow;
    }
    int used=0;
    for (int i=cur[u];~i;i=e[i].next)
    {
        int v=e[i].to;
        cur[u]=i;
        if (e[i].flow&&dep[v]==dep[u]+1)
        {
            low=dfs(v,min(flow-used,e[i].flow));
            if (low)
            {
                used+=low;
                e[i].flow-=low;
                e[i^1].flow+=low;
                if(used==flow) break;
            }
        }
    }
    return used;
}

void dinic()
{
    while (bfs())
        dfs(S,1e9);
}

int main()
{
	memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    S=n*m+3;
    T=n*m+4;
    for (int i=1;i<=n;i++)
    	for (int j=1;j<=m;j++)
    		scanf("%d",&a[i][j]);
    for (int i=1;i<=n;i++)
    	for (int j=1;j<=m;j++)
    	{
    		x=i*m-m+j;
    		if (a[i][j]==1)
    		{
    			add(S,x,1e9);
    			add(x,S,0);
   			}
    		if (a[i][j]==2)
    		{
    			add(x,T,1e9);
    			add(T,x,0);
    		}
    		if (a[i][j]<2)
    			for (int k=1;k<=4;k++)
    			{
    				if (i+di[k]<1||i+di[k]>n||j+dj[k]<1||j+dj[k]>m) continue;
    				if (a[i+di[k]][j+dj[k]]==1) continue;
    				y=(i+di[k])*m-m+(j+dj[k]);
   					add(x,y,1);
    				add(y,x,0);
   				}
    	}
    dinic();
    printf("%d
",maxflow);
    return 0;
}