题目:Unblock Me
链接:Here
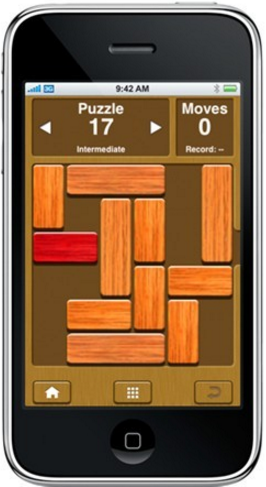
题意:一个游戏,看图就基本知道题意了,特殊的是:1. 方块长度为3或2,宽度固定是1。2. 地图大小固定是6*6,从0开始。 3. 出口固定在(6,2)。4. 每一步只能移动一个方块,但可以移动多个单位。5. 必定有解。求红色方块从出口离开的最小步骤数。
思路:
刚开始老老实实的用IDA*做,毫不犹豫的超时,样例都跑不动,剪枝也剪不了,大概知道要状态压缩,具体点就实在想不出来了,百度的题解,感觉刷新了我对状压的认识,用3位二进制表示一个方块的可变信息,然后组成一个LL型数。我写的IDA*,当时想加一个判断当前局面是否遇到过的剪枝,发现要想存状态并且快速找到很困难,现在如果用一个LL型数就可以表示局面,那就简单多了,set就可以解决。
可变信息是指在一个局面开始后会发生变化的信息,相对的不可变信息就比如某个竖立方块的列(在游戏过程中不会发生改变)、长度,因此用二维数组表示状态有很大的冗余,其实在游戏过程中竖立方块会发生变化的就只有行,而地图大小6,所以用3位二进制可以完整地保存,题目最多36/2=18个方块,所以一个LL型可以存下所有方块的信息。
接下来通过简单的位运算可以分离信息,剩下的就是bfs了,难点就在状态压缩,想到以后位置处理就简单了。
AC代码:
1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<math.h> 5 #include<set> 6 #include<map> 7 #include<list> 8 #include<stack> 9 #include<queue> 10 #include<vector> 11 #include<string> 12 #include<iostream> 13 #include<algorithm> 14 using namespace std; 15 #define lson rt<<1 16 #define rson rt<<1|1 17 #define N 20020 18 #define M 100010 19 #define Mod 1000000007 20 #define LL long long 21 #define INF 0x7fffffff 22 #define FOR(i,f_start,f_end) for(int i=f_start;i<=f_end;i++) 23 #define For(i,f_start,f_end) for(int i=f_start;i<f_end;i++) 24 #define REP(i,f_end,f_start) for(int i=f_end;i>=f_start;i--) 25 #define Rep(i,f_end,f_start) for(int i=f_end;i>f_start;i--) 26 #define MT(x,i) memset(x,i,sizeof(x)) 27 #define gcd(x,y) __gcd(x,y) 28 const double PI = acos(-1); 29 30 struct Node 31 { 32 bool type; //竖的 1 ,横的 0 33 int pos; //竖的记录行,横的记录列 34 int len; //长度 35 }v[20]; 36 37 int cal(LL s,int pos) 38 { 39 return (int)( ( s & (7LL << (pos * 3)) ) >> (pos * 3) ); 40 } 41 42 int n,red; 43 44 bool ok(LL s) 45 { 46 int rl = cal(s,red), rr = rl + v[red].len; 47 for(int i=0;i<n;i++) 48 { 49 if(v[i].type) continue; 50 if(v[i].pos <= rr) continue; 51 int il = cal(s,i), ir = il + v[i].len; 52 if(ir < 2 || il > 2) continue; 53 return false; 54 } 55 return true; 56 } 57 58 bool check(LL s,int pre) 59 { 60 int pl = cal(s,pre), pr = pl + v[pre].len; 61 for(int i=0;i<n;i++) 62 { 63 if(i == pre) continue; 64 if(v[i].type == v[pre].type) 65 { 66 if(v[i].pos!=v[pre].pos) continue; 67 int il = cal(s,i), ir = il + v[i].len; 68 if(ir<pl || pr<il) continue; 69 } 70 else 71 { 72 int il = cal(s,i), ir = il + v[i].len; 73 if( pr < v[i].pos || pl > v[i].pos || il > v[pre].pos || ir < v[pre].pos) continue; 74 } 75 return false; 76 } 77 return true; 78 } 79 80 void mov(LL &s,int pos,int x) 81 { 82 s &= ( ~( 7LL << (3*pos) ) ); 83 s |= ( (LL)x << (3*pos) ); 84 } 85 86 set<LL> mp; 87 queue<pair<LL,int> > q; 88 int bfs(LL s) 89 { 90 if(ok(s)) return 1; 91 while(q.size()) q.pop(); 92 mp.clear(); 93 q.push(make_pair(s,0) ); 94 while(q.size()) 95 { 96 s = q.front().first; 97 int d = q.front().second + 1; 98 q.pop(); 99 for(int i=0;i<n;i++) 100 { 101 int p = cal(s,i); 102 for(int j=1;p-j>=0;j++) 103 { 104 LL u = s; 105 mov(u,i,p-j); 106 if(check(u,i)==false) break; 107 if(mp.find(u)!=mp.end()) continue; 108 if(ok(u)) return d+1; 109 mp.insert(u); 110 q.push(make_pair(u,d)); 111 } 112 for(int j=1;p+v[i].len+j<=5;j++) 113 { 114 LL u = s; 115 mov(u,i,p+j); 116 if(check(u,i) == false) break; 117 if(mp.find(u)!=mp.end()) continue; 118 if(ok(u)) return d+1; 119 mp.insert(u); 120 q.push(make_pair(u,d)); 121 } 122 } 123 } 124 return -1; 125 } 126 127 int main() 128 { 129 while(~scanf("%d",&n)) 130 { 131 LL s = 0; 132 int x,y,x1,y1; 133 For(i,0,n){ 134 scanf("%*d%d%d%d%d",&x,&y,&x1,&y1); 135 if(x==x1){ // su 136 v[i].type = 0; 137 v[i].pos = x; 138 v[i].len = y1-y; 139 s |= ( (LL)y << (i*3) ); 140 } 141 else 142 { 143 v[i].type = 1; 144 v[i].pos = y; 145 v[i].len = x1-x; 146 s |= ( (LL)x << (i*3) ); 147 } 148 } 149 scanf("%d",&red); 150 printf("%d ",bfs(s)); 151 } 152 return 0; 153 }